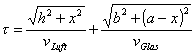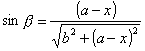|
PI X E L - Z O O |
|||||||||||||||||
| 3. Brechung | |||||||||||||||||
|
|
|||||||||||||||||
 |
Die eigentliche Bewährungsprobe für das Fermat'sche Prinzip war das Brechungsgesetz. Zwar hatten Willebrod Snel van Rojen (SNELLIUS, 1591-1626) und Rene Descartes (1596-1650) diese Formel sehr viel früher entdeckt, aber aus heutiger Sicht falsch intepretiert. Snellius hatte entdeckt, dass das Verhältnis der Sinusse von Einfalls- und Brechungswinkel eine Konstante ist, wenn ein LIchtstrahl vom dünneren Medium (z.B. Luft) in ein dichteres Medium (z.B. Wasser) wechselt. Mathematisch ausgedrückt :
|
||||||||||||||||
| Es ist wirklich verblüffend, dass Descartes trotzdem ein richtiges Ergebnis erhielt. Ein schönes Beispiel dafür, das physikalische Modelle nicht unbedingt etwas mit der "Wirklichkeit" zu tun haben müssen ! |
Descartes hatte diese Formel auch ermittelt, allerdings auf der Basis eines mechanischen Modells und unter der Annahme, dass die Lichtgeschwindigkeit im optisch dichteren Medium ( z.B. Glas, Wasser) größer ist als im dünneren Medium (z.B. Luft) - tatsächlich ist es aber genau umgekehrt ! Fermat hatte bei seiner Herleitung des Brechungsgesetzes das Prinzip der kürzesten Zeit verwendet und gleichzeitig angenommen, daß die Lichtgeschwindigkeit im optisch dichteren Medium (z.B. Glas, Wasser) langsamer ist als im dünneren (z.B. Luft). - Lesen Sie dazu den Brief von Fermat an de la Chambre, - links unten! |
||||||||||||||||
|
...... fand ich, daß mein Prinzip der Lichtbrechung zu genau derselben Proportion führte, die auch Herr Descartes aufgestellt hatte. Dieses völlig unvorhergesehene Ergebnis hat mich derart über-rascht, daß ich vor Verwunderung kaum zu mir kam. Ich habe meine algebraischen Operationen auf verschiedene Weisen wiederholt. Das Ergebnis war jedesmal dasselbe, obwohl mein Beweis auf der Annahme beruht, das Licht pflanze sich in dichteren Medien langsamer fort als in dünneren, was ich für einzig vernünftig und notwendig halte, im Gegensatz zu Herrn Descartes, der das Gegenteil behauptet. |
|||||||||||||||||
|
Also gut, - fangen wir an: Im folgenden Bild habe ich Ihnen die Situation etwas vereinfacht aufgezeichnet: |
|||||||||||||||||
|
Der "Startpunkt" des Lichtstrahls befindet sich im "Medium 1". Das Licht breitet sich in hier mit einer bestimmten Geschwindigkeit aus und wenn Fermat recht hat, dann wird es den "Endpunkt" im "Medium 2" in der kürzest möglichen Zeit erreichen. Sie sollten jetzt einmal die verschiedenen Möglichkeiten ausprobieren. Dazu klicken Sie mit der linken Maustaste auf den roten Punkt auf der Grenzfläche und 'ziehen' ihn in horizontaler Richtung hin und her. Achten Sie dabei bitte auf die Angabe der "Laufzeit". Fällt Ihnen etwas auf ? - Na klar : der kleinste Wert ergibt sich für eine abgeknickte Laufbahn. Spielen Sie 'mal ein bisschen herum, und ändern Sie vorallen auch einmal die Geschwindigkeiten im Medium 1 und im Medium 2. ( Dazu verlängern, bzw. verkürzen Sie mit gedrückter linker Maustaste die senkrechten schwarzen Pfeile.) |
|||||||||||||||||
|
Nehmen Sie die Zahlenangaben bitte nicht so genau: es geht hier zunächst nur um das Prinzip! Wenn die Geschwindigkeit im Medium 1 und im Medium 2 gleich gross sind ( das mit der Maus etwas schwierig einzustellen - aber so genau muss es auch nicht sein), dann ist der schnellste Weg zwischen Start- und Endpunkt natürliche eine gerade Linie. In allen anderen Fällen ergibt sich die kürzeste Laufzeit für eine abgewinkelte Strecke. Sie erinnern sich ? Das ist genau die Situation die ich Ihnen auf der Einleitungseite beschrieben habe: um so schnell wie möglich zu dem "Ertrinkenden" im Wasser zu gelangen, müssen Sie einen ähnlichen Weg einschlagen, - blättern Sie doch noch einmal zurück. |
|
||||||||||||||||
| Interaktives Bildschirmexperiment: Probieren Sie aus, wie der Weg des Lichtstrahls beschaffen sein muss, damit die Laufzeit minimal wird ! | |||||||||||||||||
|
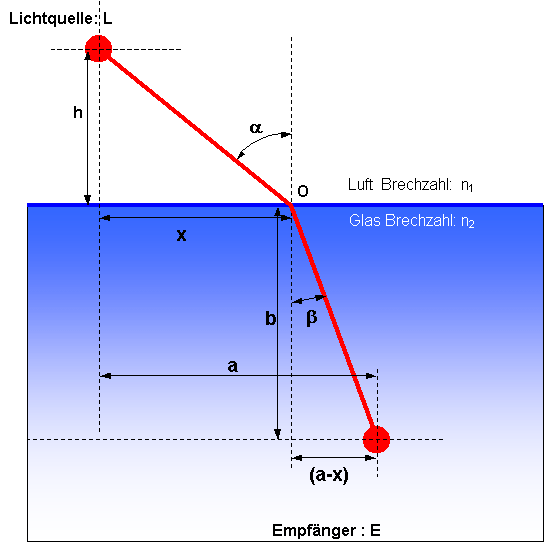
Ungefähr so könnte der Verlauf des Lichtstrahles aussehen, - wenn Fermat recht hat ! Aber "ungefähr" reicht uns nicht, wir wollen es schon genauer wissen! Ich habe mir lange den Kopf darüber zerbrochen wie ich Ihnen die Mathematik, die jetzt kommt, ersparen kann - es ist mir kein Ausweg eingefallen. Also gehen wir es an, es tut auch nicht weh ! Hier die Skizze mit den notwendigen Parametern: |
|||||||||||||||||
|
Einfallswinkel 'alpha' und Ausfallswinkel 'beta' werden gegen die sog. 'Oberflächennormale' gemessen. Die 'Oberflächennormale' ist die Senkrechte auf der Oberfläche des Glaskörpers. |
|||||||||||||||||
| Kenngrössen zur Herleitung des Brechungsgesetzes. | |||||||||||||||||
|
Da nach dem Fermat'schen Prinzip die Laufzeit |
|||||||||||||||||
|
|
|||||||||||||||||
|
Wobei vLuft und vGlas die Geschwindigkeiten des Lichtes zunächst in der Luft / Medium 1 (s.o.) und anschliessend im Glas / Medium 2 sein soll. Sie erinnern sich doch an den Satz des Pythagoras ? Mit Hilfe dieses Satzes ersetzen wir die Strecken LO und OE : |
|||||||||||||||||
|
Pythagoras ? Wie war das noch ? |
|
||||||||||||||||
Die Koordinate x beschreibt den Eintrittspunkt des Lichtstrahles auf der Glasoberfläche. Die Aufgabe besteht nun darin, den Eintrittspunkt zu finden, für den die Laufzeit  minimal wird. Zu diesem Zweck müssen wir den Ausdruck für differenzieren und anschliessend gleich Null setzten : |
|||||||||||||||||
|
Mit diesem Trick bestimmen die Mathematiker den Extremwert einer Funktion, - in unserem Fall suchen wir den Mininalwert der Laufzeit. |
 |
||||||||||||||||
|
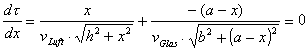Ist Ihnen etwas aufgefallen ? Nach den Regeln der Differentialrechnung haben wir zwar einen Extremwert der Funktion |
Ein Blick auf die Skizze im Bild oben zeigt, daß sich diese Beziehung durch die Einführung von Einfalls- und Ausfallswinkel erheblich vereinfachen läßt. Aus dem Bild lässt sich ablesen, dass der Sinus des Einfallswinkels sich auch so ausdrücken lässt:
Der Sinus des Ausfallswinkels ergibt sich aus:
|
||||||||||||||||
| Wenn Sie diese Ausdrücke für den Einfallswinkel und den Ausfalsswinkel in die Gleichung darüber einsetzen, dann wird die Angelegenheit plötzlich sehr übersichtlich: | |||||||||||||||||
 |
|||||||||||||||||
| Oder vielleicht gefällt es Ihnen so besser ..... | |||||||||||||||||
 |
|||||||||||||||||
| 'Sinusse' - gibt es diesen Plural ? | d.h., die 'Sinusse' - der beiden Winkel verhalten sich wie die Ausbreitungsgeschwindigkeiten in den jeweiligen Materialien. | ||||||||||||||||
|
Uff, das war's : das ist das Brechungsgesetz ! Und hier noch eine kleine interaktive Grafik, die Ihnen ein Gefühl für das Brechungsgesetzt vermitteln soll. |
|||||||||||||||||
| Verändern Sie die Richtung des einfallenden Strahls. 'Klicken' Sie dazu mit gedrückter linker Maustaste auf den roten Punkt am Ende des Strahls. Die Lichtgeschwindigkeit im Medium 2 können Sie durch 'ziehen' an der Spitze des schwarzen Pfeils auf der linken Seite beeinflussen.
Wenn Sie die Lichtgeschwindigkeiten in beiden Medien gleich gross machen dann verschwindet der Brechungseffekt. |
|
||||||||||||||||
| Interaktives Bildschirmexperiment: Erproben Sie die Auswirkung des Brechungsgesetzes. | |||||||||||||||||
| Und jetzt müssen wir uns noch über etwas anderes unterhalten:
... das Verhältnis der Geschwindigkeiten |
|||||||||||||||||
 |
|||||||||||||||||
|
Brechungsindex einiger Materialien gegen Luft :
|
Obwohl der Brechungsindex eigentlich das Verhältnis der Ausbreitungsgeschwindigkeiten in zwei verschiedenen Materialien kennzeichnet, haben Sie vielleicht schon davon gehört, daß man oft auch vom Brechungsindex eines einzigen Materials spricht. Hier hat sich eine gewisse Schlampigkeit in der Bezeichnung eingeschlichen, - gemeint ist nämlich auch hier eine Verhältnisangabe, und zwar die Vakuumlichtgeschwindigkeit vo im Verhältnis zur Geschwindigkeit des Lichtes im jeweiligen Material. Der Brechungsindex von Glas müßte danach so definiert werden: | ||||||||||||||||
 Oder etwas allgemeiner: |
|||||||||||||||||
 |
|||||||||||||||||
|
Mit anderen Worten: der Brechungsindex zwischen zwei Materialen läßt aus den Brechungsindizes der einzelnen Materialien gegenüber einem dritten, z.B. dem Vakuum, bestimmen. Unter Verwendung dieser Definitionen schreibt sich das Brechungsgesetz dann so: |
|||||||||||||||||
|
|
|||||||||||||||||
| Speziell für den Übergang Luft / Glas gilt: | |||||||||||||||||
 |
|||||||||||||||||
| da der Brechungsindex von Luft sehr dicht bei '1' liegt (nLuft = 1,000276 s.o.). | |||||||||||||||||
| Wo liegt nun der substanzielle Unterschied zum Brechungsgesetz von Snellius ? Snellius hatte auf rein emprischem Weg herausgefunden, daß das Verhältnis der Sinusse von Einfalls- und Brechungswinkel eine Konstante ist, also | |||||||||||||||||
 |
|||||||||||||||||
| (Ich hatte das bereits eingangs erwähnt.) Für den Übergang Luft Wasser beträgt diese Konstante 1,33.
Ist das nicht die gleiche Aussage wie die des oben oben hergeleiteten Brechungsgesetztes ? Nein ! - Durch die Fermat'sche Herleitung des Brechungsgesetzes wird deutlich, daß sich hinter der Konstanten ( 'const' ) das Verhältnis der Ausbreitungsgeschwindigkeiten verbirgt. Wenn man also für zwei Materialien die Ausbreitungsgeschwindigkeiten misst, dann ist es nach der Fermat'schen Formulierung sofort möglich, eine Voraussage über die Lichtbrechung zu ma-chen, - genau das leistet die Snellius-Formel nicht. |
|||||||||||||||||
|
|
|||||||||||||||||
|
Optische Weglänge ! Wichtig ! |
Bei dieser Gelegenheit sollten wir kurz den Begriff der "optischen Weglänge" erläutern.
Als optische Weglänge bezeichnet man das Produkt aus der geometrischen Strecke 'L' die ein Lichtstrahl zwischen zwei Punkten zurücklegen muss und dem Brechungsindex des Mediums nmedium in dem der Lichtstrahl verläuft: L * nmedium Ein Beispiel: Wenn ein Lichtstrahl im Vakuum eine Strecke von 10 cm zurücklegt, dann beträgt die optische Weglänge Lopt-vac = L * nvac = 10 * 1 = 10, denn der Brechungsindex im Vakuum beträgt nvac = 1. Im Wasser entspricht die geometrische Strecke von 10cm einer optischen Weglänge von : Lopt-Wasser = L * nWasser = 10 * 1,33 = 13,3 cm ! Als ich soeben die optische Weglänge im Wasser in der Einheit "cm" angegeben habe, habe ich einen Moment gezögert. Formal ist der Brechungsindex, also Verhältnis von zwei Geschwindigkeiten, s.o., dimensionslos und für die Dimension der optischen Weglänge, ergibt sich deshalb einfach eine Länge. So weit so einfach ! Aber geht es Ihnen nicht auch so: Mit dem Begriff "Weglänge" verbinden wir die Vorstellung einer geometrischen Grösse. Ein Weglängenstück von 10 cm bleibt 10 cm, egal ob es im Vakuum, im Wasser oder im Glas liegt. Gemeint ist mit dem Begriff der "optischen Weglänge" auch etwas anderes: Obwohl der Begriff "optische Weglänge" eine geometrische Grösse suggeriert, ist damit viel eher eine Masszahl für die Laufzeit des Lichtstrahls in den verschiedenen Medien gemeint. |
||||||||||||||||
|
|
|||||||||||||||||
| So und weil es so schön war, jetzt noch eine Zugabe:
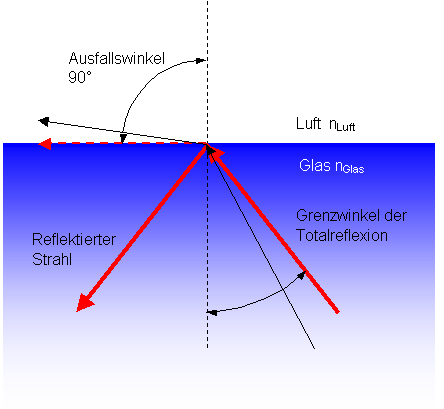
Zum Thema Brechung passt nämlich auch sehr gut das Thema Totalreflexion. Stellen Sie sich bitte vor, der Strahl im Bild oben verläuft genau entgegengesetzt, also vom Glas in die Luft. Wenn nun der Einfallswinkel (jetzt auf der Glasseite!) immer weiter vergrößert wird, dann tritt schließlich die Situation ein, daß der Ausfallwinkel größer als 90° werden müßte. Das ist genau der Punkt an dem der Lichtstrahl nicht mehr in die Luft austritt, sondern vollständig in das dichtere Medium (Glas) zurück reflektiert wird. Der Grenzwinkel der "Totalreflexion" ist erreicht. |
|||||||||||||||||
| Prinzipskizze zur Totalreflexion. | |||||||||||||||||
| Mit Hilfe des oben hergeleiteten Brechungsgesetzes läßt sich dieser Grenzwinkel im optisch "dichteren" Medium sehr leicht berechnen:
Wenn der Ausfallswinkel 90° beträgt, dann nimmt der Sinus des Ausfallswinkels den Wert '1' an. Das Brechungsgesetzt ändert sich dann zu: |
|||||||||||||||||
 |
|||||||||||||||||
Wenn man diesen Ausdruck nach  total auflöst, dann ergibt sich:
Nimmt man an, dass der Brechungsindex der Luft sehr nah bei '1' liegt, dann läßt sich die Angelegenheit weiter vereinfachen :
d.h., bei einem Brechungsindex von 1,5 (BK7-Glas) ist der Grenzwinkel der Totalreflexion: |
|||||||||||||||||
| Im nächsten Kapitel : was bedeutet es eigentlich, wenn man von der Fokussierung eines Lichtstrahls spricht ? | |||||||||||||||||
wird im allgemeinen als 'Brechungsindex' n12 eines bestimmten Mediums (1) gegenüber einem anderen (2) bezeichnet, also:
