|
PI X E L - Z O O |
|||||||||||||||||
|
5. Asphärische LInsen |
|||||||||||||||||
|
|
|||||||||||||||||
|
....Sie haben gerade im Kapitel 4 gelesen, dass es grundsätzlich möglich sein sollte, durch ein geeignet geformtes "optisches Bauelement" sämtliche Strahlen eines Lichtbündels auf einen Punkt, den "Bildpunkt" zu fokussieren. Nun wäre es natürlich ganz interessant zu wissen, wie die Oberfläche eines Bauelementes beschaffen sein muß, damit das auch klappt. |
|||||||||||||||||
|
Machen wir es uns möglichst einfach und nehmen zunächst an, daß zwischen der Quelle und dem Empfänger nur eine Grenzfläche existiert. |
|||||||||||||||||
|
Im folgenden Bild ist die Situation dargestellt: |
|||||||||||||||||
|
|
|||||||||||||||||
|
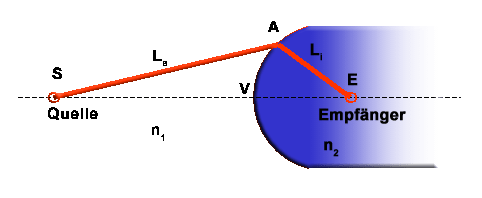
Strahlverlauf durch eine asphärische Fläche.
|
|||||||||||||||||
|
So, - wie war das noch mit der Fermat'schen Prinzip ? Der Lichtstrahl wird zwischen Quelle ( S ) und Empfänger (E) den schnellsten Weg wählen. Wenn wir nun so etwas wie eine "Abbildung" der Licht-Quelle am Ort des Empfängers reralisieren wollen, dann hilft es uns wenig, wenn dieser kürzeste Weg nur für einen der vielen Strahlen existiert, - z.B. für den im obigen Bild eingezeichneten, wobei man rein gefühlsmässig sagen würde, dass es sich dabei um einen längeren Weg handelt - und alle anderen erfüllen diese Bedingung nicht. |
|||||||||||||||||
| Sie erinnern sich ? Die "optische Weglänge" (OWL) ist eine Maß für die Lauftzeit. |
Eine Abbildung mit möglichst grosser Bildhelligkeit kann erst dann entstehen, wenn eine möglichst grosse Anzahl von Lichtstrahlen daran beteiligt ist. D.h. die Fermat'sche Bedingung darf nicht nur für einen - z.B. für den oben gezeigten - Pfad, erfüllt sein, sondern auch für alle möglichen andreren Pfade. Die optische Weglänge, die sich aus dem Produkt der geometrischen Wegstrecke (La + Li im obigen Bild) multipliziert mit dem jeweiligen Brechungsindex ( n1 bzw. n2) ergibt, muss deshalb für alle möglichen Verläufe gleich sein:
|
||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Das ist nun eine spannende Situation: | ||||||||||||||||
| Wie muss denn die Grenzfläche zwischen den beiden Medien geformt sein, damit alle Strahlen exakt die gleiche optische Wegstrecke vor sich haben ? Egal ob sie auf einem stark abgewinkelten, oder auf direktem (geradem) Pfad von der Quelle zum Empfänger laufen. | |||||||||||||||||
| Lassen Sie uns zu dieser Frage ein kleines Experiment am Bildschirm machen: | |||||||||||||||||
| Bitte nehmen Sie die Zahlenangaben nicht allzu ernst. Es geht uns hier nur um das Prinzip und (noch) nicht die exakte Beschreibung. Wichtig zum Verständnis des "Bilschirm-Experimentes" ist lediglich die Tatsache, dass der rechte Teil des Lichtstrahls in einem Medium mit grösserem Brechungsindex, also mit kleinerer Geschwindigkeit (!), verläuft. | In der folgenden Skizze sehen Sie eine symbolische Darstellung des Strahlverlaufes: der linke Teil (hellrot) repräsentiert einen Strahl in einem Medium mit dem Brechungsindex n2 = 1 und der rechte Teil (dunkelrot) verläuft in einem Medium mit dem Brechungsindex n2 = 1,5. | ||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
|
||||||||||||||||
| Interaktives Bildschirmexperiment: Durch Verschieben des roten (Knick-)Punktes finden Sie heraus welche Strahlverläufe die gleiche optische Weglänge haben. | |||||||||||||||||
|
Klicken Sie nun auf den roten Punkt zwischen den beiden Teilstrahlen und ziehen Sie den Punkt (mit gedrückter linker Maustaste!) auf dem Bildschirm beliebig hin und her. Achten Sie dabei bitte auf die Anzeige "Opt. Weglänge = XX,xx (rel.Einh.)" oben links im Bild. Es wird Sie kaum wundern, dass sich die optische Weglänge in Abhängigkeit von der Mausposition verändert. |
|||||||||||||||||
|
Aber nun versuchen Sie doch bitte einmal eine der vorgegebenen Grenzflächen (Gerade, Ellipse, Kreis) mit dem roten Punkt abzufahren ! |
|||||||||||||||||
| Sie sollten etwas großzügig mit sich selbst sein ! - es ist nicht ganz leicht den Mauszeiger so zu positionieren, dass der Wert für die optische Weglänge überall gleich ist. |
Merken Sie was ? - Die "liegende" Ellipse, mit der etwas dicker gezeichneten Kontur, scheint etwas besdonderes zu sein. Egal an welcher Stelle Sie den roten Punkt mit dem Mauszeiger plazieren, die optische Weglänge ist immer gleich ! |
||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Sie haben die Form der Grenzfläche entdeckt, bei der sämtliche möglichen Strahlverläufe zwischen der Quelle und dem Empfänger die gleiche optische Weglänge aufweisen. Mit einer so geformten Grenzfläche ist eine Abbildung möglich ! |
||||||||||||||||
|
|
|||||||||||||||||
| O.K. - diejenigen von Ihnen, denen dieses qualitative Wissen genügt, können jetzt mit einem KLICK den theoretischen Teil überspringen und gleich einige praktische Linsenformen betrachten. Oder wollen Sie zum nächsten Kapitel wechseln ?
Für die übrigen folgt eine (etwas) genauere Begründung: |
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
| Sie erinnern sich?
Erläuterungen in Grau sind für das Verständnis der weiteren Kapitel nicht unbedingt notwendig ! |
Unser Bildschirm-Experiment hat uns bereits auf die Idee gebracht, dass es sich bei der Form der Grenzfläche möglicherweise um ein Ellipsoid handeln könnte! Wir werden diese Vermutung 'mal als richtig unterstellen und nachweisen, dass ein Ellipsoid die Fermat'sche Bedingung tatsächlich erfüllt, oder anders ausgedrückt: Sämtliche Strahlverläufe zwischen LIchtquelle und Empfänger sind gleich lang, egal an welchem Punkt der Lichtstrahl die Grenzfläche zwischen den beiden Medien passiert. Mathematisch ausgedrückt würde man schreiben: |
||||||||||||||||
| Damit ist natürlich noch nicht geklärt, ob nicht auch noch andere Grenzflächenformen die Fermat'sche Bedingungen erfüllen, .... aber das ist uns jetzt wurscht ! Wenn es noch andere Lösungen geben sollte, - umso besser! Wir sind ja schon froh, wenn es überhaupt eine gibt ! |
|
||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Zur weiteren Vereinfachung wollen wir annehmen, daß die Quelle S ins Unendliche rückt, so daß die Strahlen parallel an der Grenzfläche eintreffen und sich innerhalb des Ellpoids in einem Punkt F2 treffen. Die Forderung, dass die Fermat'sche Bedingung für alle möglichen Strahlverläufe erfüllt sein soll, bedeutet in diesem Fall, dass die optische Weglänge für sämtliche parallel einfallenden Strahlen bis hin zum gemeinsamen Bildpunkt F2 gleich sein müssen. (In diesem Spezialfall bezeichnet man den Bildpunkt F2 als Brennpunkt). |
||||||||||||||||
|
|
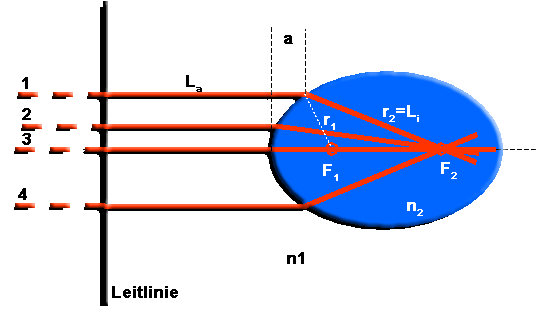
Bitte betrachten Sie im folgenden Bild z.B. die Strahlen 1 und 3. Auf seinem Weg von der ("unendlich weit" entfernten) Quelle zur Grenzfläche muss Strahl 1 eine längere Wegstrecke zurücklegen als Strahl 3. Da unendliche Entfernungen immer etwas unhandlich sind, wollen wir als Bezugslinie für den Abstand La zur Grenzfläche die sog. "Leitlinie" des Ellipsoids verwenden. Die uns interessierenden Laufwegveränderungen zwischen den verschiedenen Strahlen treten ja nur in diesem letzten Teilstück auf. Der Hauptgrund aber, warum wir die Leitlinie hier einführen, ist die Tatsache, das es einige sehr einfache Zusammenhänge zwischen den Parametern der Ellipse (z.B. die beiden Radien r1 und r2 ) und dem Abstand La zur Leitlinie gibt . |
||||||||||||||||
| Bitte beachten Sie: Die Lichtstrahlen verlaufen von einem Medium mit dem Brechungsindex n1 (z.B. Luft) in ein Medium mit dem grösseren Brechungsindex n2 (z.B. Glas)! |
|
||||||||||||||||
|
Brennpunkt einer ellipsoidförmigen brechenden Fläche ( n1 < n2).
|
|||||||||||||||||
|
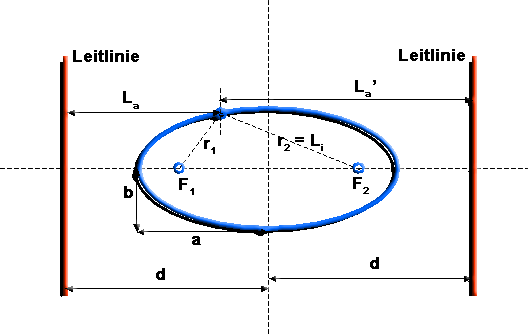
Kennen Sie noch die Definitionen aus der analytischen Geometrie für die Ellipse ? Hier zur Erinnerung - und soweit wir sie für diesen Teil der geometrischen Optik benötigen - einige der Formeln und Begriffe: |
|||||||||||||||||
|
 |
||||||||||||||||
| Kenngrössen der Ellipse. | |||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
|
||||||||||||||||
|
Definition: Die Ellipse ist der geometrische Ort aller Punkte, für die die Summe der Abstände von zwei gegebenen festen Punkten (Brennpunkten) konstant ist.: |
r 1 + r2 = const
|
||||||||||||||||
| Definition: Leitlinien sind Geraden, die zur kleinen Achse b parallel sind und von dieser den Abstand d = a / e haben, wobei e die numerische Exzentrizität ist: |
d = a / e
|
||||||||||||||||
| Zusammenhang zwischen numerischer Exzentrizität e, den Abständen r1/2 und La La'. |
e = r1 / La = r 2 / La'
|
||||||||||||||||
|
Bei einer Ellipse gilt immer: |
e < 1 |
||||||||||||||||
|
Soweit die geometrischen Eigenschaften einer Ellipse, - dieses Wissen wollen wir jetzt einsetzen.
|
|||||||||||||||||
|
Ausgangspunkt ist die Beziehung :
|
r 1 + r2 = const | ||||||||||||||||
| Aus den oben gezeigten Skizzen können wir ablesen: | r2 = Li | ||||||||||||||||
|
der Ausdruck für die numerische Exzentrizität e = r1 / La = r 2 / La' (s.o.) lässt sich umformen: |
r1 = e . La |
||||||||||||||||
| Ersetzt man man in der Beziehung r1 + r2 = const r1 und r2 durch die zuletzt beschriebenen Entsprechungen, dann erhält man: | Li + e .La = const | ||||||||||||||||
|
und nach einer Multiplikation mit n2 ergibt sich daraus : |
|
||||||||||||||||
|
Diese Beziehung ist identisch mit der Fermat'schen Bedingung wenn man für die Exzentrizität e = n1/n2 einsetzt. Da bei dem hier diskutierten Fall der Brechungsindex n1 kleiner als n2 sein soll, ist e < 1, woraus folgt, daß die Form der Grenzfläche tatsächlich eine Ellipse ist. |
|||||||||||||||||
|
|
|||||||||||||||||
| Wir sollten die gleiche Überlegung noch einmal anstellen, diesmal aber für den Fall, daß ein divergierendes Strahlenbündel durch eine geeignet geformte Grenzfläche in ein parallel verlaufendes Strahlenbümdeln verwandelt wird. Um das Ergebnis gleich vorweg zu nehmen - die Form der Grenzfläche, die dies leistet, ist ein Hyperboloid - und um die Sache zu vereinfachen, soll nur gezeigt werden, daß auch hier die Fermat'sche Bedingung ( "....die Zeit für alle Strahlverläufe muß gleich sein...." ) erfüllt ist. | |||||||||||||||||
|
|
|||||||||||||||||
|
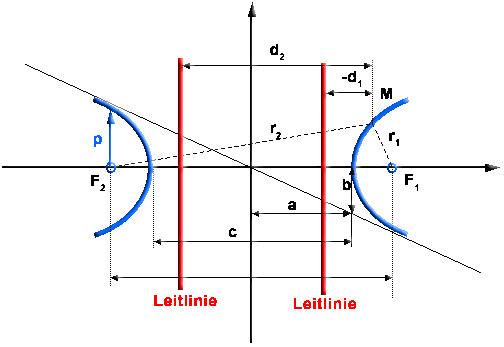
Aber bevor wir das tun, muss ich Sie auch hier an einige Zusammenhänge aus der analytischen Geometrie für die Hyperbel erinnern: Hyperbelgleichung: Brennpunkteigenschaft: e = c/a > 1 Leitlinieneigenschaft: |
 |
||||||||||||||||
|
Kenngrössen der Hyperbel.
|
|||||||||||||||||
| So, und nun der Strahlverlauf : Wie gesagt, diesmal möchten wir erreichen, dass ein divergentes Strahlenbündel nach dem Entritt in das Medium mit dem Brechungsindex n2 als paralleles Strahlenbündel weiter läuft und unsere Vermutung geht dahin, dass dies von einer hyperbolisch geformten Grenzfläche geleistet wird. | |||||||||||||||||
| zurück zum Inhaltsverzeichnis zur Fotoseite "pixel-zoo" nach oben |
 |
||||||||||||||||
|
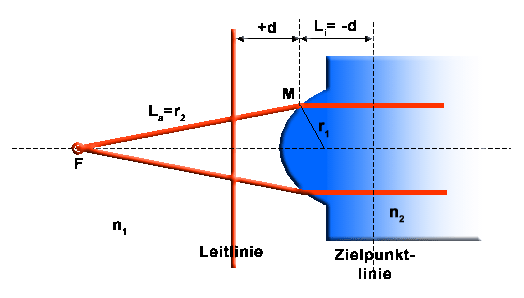
Strahlverlauf durch eine hyperboloidförmige brechende Fläche. (Der Abstand der Leitlinie von dem Punkt M auf der Oberfläche ist +d. Li = -d ist der Abstand der Zielpunkte innerhalb des Hyperboloids .)
|
|||||||||||||||||
| Für die Brennpunkteigenschaft der Hyperbel gilt : | r2 - r1 = const | ||||||||||||||||
| Im letzten Bild ist r2 = La der Abstand zwischen dem Startpunkt F und dem Auftreffpunkt M auf der Oberfläche.Für r1 läßt sich die Leitlinieneigenschaft der Hyperbel benutzen r1 = e.d. Wenn man berücksichtigt, daß sich die Zielpunktlinie im Abstand Li = -d vom Auftreffpunkt befindet, dann läßt sich die obige Brennpunkteigenschaft der Hyperbel so umformulieren: | La + e . Li = const | ||||||||||||||||
| Um aus dieser rein geometrischen Beziehung einen Ausdruck für die optischen Strecken zu formen, wird diese Gleichung nun noch auf beiden Seiten mit dem Brechungsindex n1 multipliziert: | n1 . La + e . n1 . Li = n1 . const = const | ||||||||||||||||
| Für e = n2/n1 > 1 entspricht dies exakt der Fermat'schen Bedingung. Die Tatsache, daß die numerische Exzentrizität e größer als '1' ist macht deutlich, daß es sich in diesem Fall um ein Hyperboloid handeln muß. | |||||||||||||||||
| Die Umkehrbarkeit bzw. die Reziprozität bei der Ausbreitung von Lichtstrahlen steckt ja bereits im Fermat'schen Prinzip, - denn danach wird lediglich gefordert, daß der Weg auf die kürzest mögliche Art zurückgelegt wird (die richtigere Formulierung dieses Prinzips finden Sie auf Seite ..... ) , - in welche Richtung der Lichtstrahl verläuft ist dabei vollkommen 'wumpe'.
Aber wie so oft in der Physik ( - und im Leben ! ): Immer wenn man behauptet , daß irgend etwas sich 'grundsätzlich' so und nicht anders verhält, dann wird man sehr schnell mit den Ausnahmen von der Regel konfrontiert: So ist es auch bei der Umkehrbarkeit (Reziprozität) des Lichtweges; von Helmholtz stammt die Erkenntnis, daß diese Umkehrbarkeit des Lichtweges z.B. nicht mehr gilt, wenn ein Magnetfeld ins Spiel kommt: ....... aber lassen wir das, das führt zu weit ! |
Sehr wichtig für die Realisierung von konkreten Linsen ist die Tatsache, daß Strahlverläufe in der Optik grundsätzlich umkehrbar sind. D.h. der Strahl kann z.B. im Innern eines Ellipsoids aus Glas starten und dann außerhalb parallel zur optischen Achse weiterlaufen. In den Bildern sind deshalb absichtlich auch keine Pfeile eingezeichnet, die die Ausbreitungsrichtung andeuten. | ||||||||||||||||
|
|
|||||||||||||||||
|
Langer Rede, kurzer Sinn : Wir haben gezeigt, daß es möglich ist, unter Beachtung des Fermat'schen Prinzips, die Grenzfläche zwischen zwei optischen Medien so zu formen, daß ein divergierendes Strahlenbündel parallel ausgerichtet (Hyperboloid) und ein paralleles Strahlenbündel auf einen Punkt (Ellipsoid) fokussiert werden kann.
|
|||||||||||||||||
|
Mit dieser Kenntnis ist es nun möglich 'Linsen' zu konstruieren, bei denen der Gegenstandpunkt und der Bildpunkt in demselben Medium ( i.a. Luft) liegen. Wir wollen 'mal zwei Beispiele näher betrachten: |
|||||||||||||||||
|
1. Hyperbolische Bikonvexlinse: |
|||||||||||||||||
|
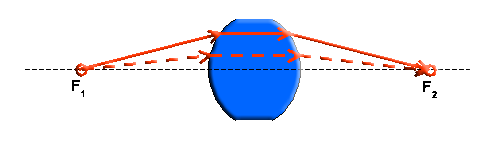
Hyperbolische Bikonvexlinse
|
|||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Im obigen Bild ist eine Bikonvexlinse dargestellt, die zwei hyperbolische Grenzflächen hat. Ein vom Brennpunkt F1 divergent austretendes Strahlenbündel trifft auf die hyperbolische Grenzfläche und wird - so wie bereits im Bild "Strahlverlauf durch eine hyperboloidförmige brechende Fläche" dargestellt - innerhalb des Glaskörpers parallel zur optischen Achse weiterlaufen. Als nächstes trifft das Strahlenbündel auf die zweite Hyperboloidfläche und wird, in Umkehrung desselben Strahlenganges, auf den Brennpunkt F2 fokussiert.
|
||||||||||||||||
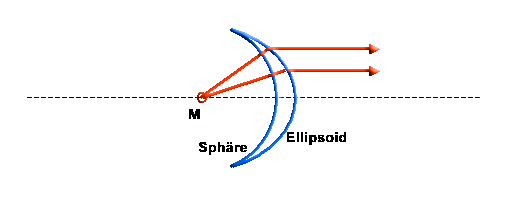
| Im nächsten Bild ist eine Linse dargestellt, die aus einer sphärischen / kugelförmigen Fläche und einem Ellipsoid besteht. Diese Flächenkombination macht aus einem dirvergierenden Strahlenbündel ein paralleles, - aber nur unter der Bedingung, dass der Ausgangspunkt des Strahlenbündels im Mittelpunkt der Kugelfläche liegt. Wenn das der Fall ist, dann trifft jeder Teilstrahl senkrecht auf die erste sphärische Fläche und verläuft von dort geradlinig weiter bis zur zweiten, elliptisch geformten Oberfläche. *) Hier passiert nun genau das, was im Bild "Brennpunkt einer ellipsoidförmigen brechenden Fläche" dargestellt ist - die in einem optisch dichteren Medium (z.B. Glas) divergierend verlaufenden Strahlen werden nach dem Passieren einer ellipsoidförmigen Grenzfläche parallel ausgerichtet.
*) Da die Strahlen senkrecht auf die sphärische Grenzfläche treffen, findet hier keine Brechung statt ! |
|||||||||||||||||
|
2. Sphäroelliptische Konvexlinse : |
|||||||||||||||||
| Sphäroelliptische Konvexlinse | |||||||||||||||||
|
Achtung merken !!! |
Konvexe Linse : in der Mitte dicker als am Rand ('convexus' = gewölbt) |
||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Durch Kombination von Ellipsoiden und Hyperboloiden kann also jede beliebige Linse hergestellt werden. Dabei ergibt sich allerding eine Schwierigkeit: asphärischen Oberflächen sind sehr schwierig herzustellen. Aus gepreßtem Glas oder Kunststoff findet man sie häufig als Kondensorlinsen in Projektionsapparaten. Sie lassen sich auch mit computergesteuerten Poliermaschinen herstellen, aber als Präzisionsbauteil sind sie immer noch sehr aufwendig und teuer.
|
||||||||||||||||
|
|
|||||||||||||||||