|
PI X E L - Z O O |
|||||||||||||||||||||||||
|
6. Brechung an einer Kugelfläche |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
Ich muss Sie warnen: dieses Kapitel ist ziemlich trocken und langweilig ! (Da kann auch der lustige Schneemann links nichts mehr retten.)
Der Strahlverlauf zwischen zwei Medien (z.B. Luft und Wasser), die durch eine kugelförmige Grenzfläche von einander getrennt sind, ist eigentlich nur für den Schneemann in der Glaskugel interessant . Ein weiteres 'wichtiges' und oft zitiertes Beispiel ist der Fisch in einem kugelförmigen Aquarium ! Sie haben sich doch bestimmt schon häufig mit der Frage herumgequält, wie dieser Fisch seine Umwelt wahrnimmt ? Na sehen Sie, - es wird Zeit diese Frage zu beantworten. |
||||||||||||||||||||||||
|
Bevor wir anfangen habe, ich doch noch eine etwas seriösere Begründung, warum wir uns mit dem Strahlverlauf durch eine Kugelfläche befassen sollten: |
|||||||||||||||||||||||||
|
Obwohl die ideale Grenzfläche für die Fokussierung eines Strahlenbündels eine Asphäre (Ellipse oder Hyperboloid) ist,- wir haben das im letzten Kapitel (Kapitel 5 ) ausführlich diskutiert - werden in der Praxis häufig kugelförmige Linsen benutzt. Kugeloberflächen sind nämlich sehr viel einfacher und damit billiger herzustellen als asphärische Flächen. Es macht deshalb vielleicht doch etwas Sinn, wenn wir uns mit der Kuglefläche und ihren Eigenschaften als optischem Element beschäftigen. |
|||||||||||||||||||||||||
| Ich könnte Sie übrigens gut verstehen, wenn Sie sich nur 'mal kurz den Effekt ansehen und den ganzen übrigen Kram überspringen wollen. Wird für die folgenden Kapitel auch nicht unbedingt gebraucht. Versprochen !
Also gut ! Machen Sie es sich leicht - klicken Sie hier. |
|||||||||||||||||||||||||
|
Fangen wir an ! Es ist wirklich ganz einfach - alles was wir benötigen ist die folgende Dreiecksgeometrie: |
|||||||||||||||||||||||||
|
Für die Beschreibung der Brechung eines Lichtstrahls an einer Kugeloberfläche halte ich mich im folgenden an die Darstellung von Richard P. Feynman "Vorlesungen über Physik", Bd.1. |
|||||||||||||||||||||||||
|
Kenngrössen für die Geometrie einer Linse mit kugelförmigen Grenzflächen. |
|||||||||||||||||||||||||
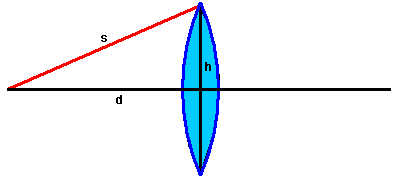
| 'paraxial' Strahlen, - das sind die Strahlen, die in der Nähe der optischen Achse verlaufen ! Danach wäre der mit 's' gekennzeichnete Strahl im obigen Bild kein paraxialer Strahl. |
Um die Abbildungsfehler einer sphärischen Fläche möglichst klein zu halten, soll im folgenden nur von den sog. paraxialen Strahlen die Rede sein. |
||||||||||||||||||||||||
|
Die gesamte Geometrie und die mit den paraxialen Strahlen verbundene Näherung ist im obigen Bild dargestellt. Mehr ist tatsächlich nicht notwendig! |
|||||||||||||||||||||||||
| In der Form
a2 + b2 = c2 haben Sie Herr Pythagoras in der Schule kennengelernt, - Sie erinnern sich bestimmt ! |
Es geht nämlich nur um die Frage, um wieviel länger ist der 'schräg' verlaufende Strahl 's' gegenüber dem direkten 'd'. Das lässt sich leicht ermitteln. s, d und h bilden ein rechtwinkliges Dreieck. Auf ein solches Dreieck können wird den Satz des Pythagoras anwenden: s2 = d2 + h2 . Oder etwas umgestellt: |
||||||||||||||||||||||||
|
s2 - d2 = h2 |
|||||||||||||||||||||||||
|
es gilt:
s2 - d2 = (s+d).(s-d) |
bzw. : (s-d).(s+d) = h2 (s-d) = h2 / (s+d) |
||||||||||||||||||||||||
| Näherung für Paraxialstrahlen : wenn s ~ d ist, dann gilt (s + d) ~ 2s ! |
|||||||||||||||||||||||||
| 's' bzw. 'd' werden in der Literatur auch als "Schnittweite" bezeichnet. Da bei achsennahen Strahlen 's' und 'd' ohnehin annähernd gleich sind, ist die Bezeichnung nicht ganz einheitlich. |
Mit der Näherung für achsennahe Strahlen (s + d) ~ 2s läßt sich die Wegdifferenz wdiff zwischen dem schräg verlaufenden und dem direkten Strahl so schreiben: wdiff = (s - d) = h2 / (s + d) |
||||||||||||||||||||||||
|
wdiff ~ h2 / 2s |
|||||||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
|||||||||||||||||||||||||
|
Im Fall der Kugelfläche kann es hierbei allerdings nur um die Frage gehen, wie gut (bzw. wie schlecht) die Annäherung an den Idealfall der Asphäre gelingt. (Kapitel 5) |
Nach dem Fermat'schen Prinzip müssen nun sämtliche Strahlverläufe zwischen Quelle und Empfänger (zeitlich) gleich lang sein. Wie kann das gelingen ? Sie kennen das Konzept bereits: ein die Laufzeit verzögerndes Medium muß so zwischen Quelle und Empfänger angeordnet werden, daß der direkte Weg (schwarz) genauso lang ist wie der abgeknickte (rot). |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
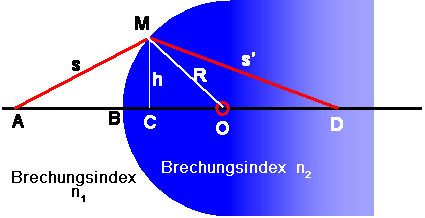
| Brechung an einer kugelförmigen Grenzfläche. (Kenngrössen) | |||||||||||||||||||||||||
|
Optische Weglänge: Produkt aus geometrischer Entfernung und Brechungsindex ! |
Der Strahlverlauf durch eine kugelförmige Grenzfläche ist im obigen Bild dargestellt. In der Näherung, die wir hier betrachten, interessieren uns nur die beiden Dreiecke AMC und CMD. Die optische Weglänge des direkt von A nach D verlaufenden Strahls beträgt:
(n1 . AC + n2 . CD ) Die optische Weglänge des abgeknickten Strahles beträgt: (n1 . AM + n2 . MD ) |
||||||||||||||||||||||||
|
Wir hatte bereits abgeschätzt, daß die Strecke AM um h2 / 2s länger ist als die Strecke AC. (Siehe oben !) Nach derselben Überlegung ist MD um h2 / 2s' länger als CD . Daraus folgt, daß die optische Weglänge des abgeknickten Strahlengangs (rot) insgesamt um: länger ist, als der auf dem direkten Weg verlaufende Strahl. |
|||||||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Um dem Fermat'schen Prinzip zu genügen, muß die optische Weglänge zwischen dem abgeknickten und dem direkten Strahl aber gleich groß sein! Ein etwas genauerer Blick auf die Skizze im obigen Bild zeigt, wie das gelingen kann - bei der Herleitung der Weglängendifferenz wges haben wir nämlich eine Kleinigkeit übersehen: Auf dem Weg von A nach C läuft der 'direkte Strahl' zwischen B und C bereits durch das Medium mit dem dichteren Brechungsindex n2 . Auf diesem Teilstück hatten wir fälschlicherweise mit einem Brechungsindex n1 und einer optischen Weglänge von n1.BC gerechnet. Tatsächlich beträgt sie aber n2.BC , ist also um (n2 - n1).BC größer als n1.BC . |
||||||||||||||||||||||||
|
|
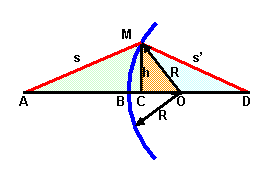
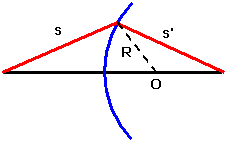
So, jetzt müssen wir nur noch herausfinden wie groß die Wegstrecke BC ist. Schauen Sie sich dazu nocheinmal das obige Bild , oder die kleine Skizze links an.
|
||||||||||||||||||||||||
|
|
R ist der Radius der Kugeloberfläche, - das wussten Sie schon ! R, CO und h bilden ein rechwinkliges Dreieck und genau wie oben, wenden wir den Satz des Pythagoras an: R2 = CO2 + h2 oder: R2 - CO2 = h2 und wenn Sie sich an Ihre Algebra-Stunden in der Schule erinnern, dann können Sie statt dessen schreiben: (R - CO).(R + CO) = h2 (R - CO) ist identisch mit der gesuchten Strecke BC und da CO ungefähr so gross wie R ist - zumindest für achsennahe (paraxiale) Strahlverläufe - können Sie (R + CO) durch 2R ersetzten, also: BC . 2R ~= h2, bzw: BC ~= h2 / 2R
|
||||||||||||||||||||||||
|
Damit die beiden Wegstrecken AMD (rot) und ACD (schwarz) tatsächlich gleich groß sind, muß die Bedingung:
|
|||||||||||||||||||||||||
|
wges = (n2 - n1).BC
|
|||||||||||||||||||||||||
| bzw.: | |||||||||||||||||||||||||
|
n1.(h2 / 2s) + n2.(h2 / 2s') = (n2 - n1).(h2 / 2R)
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
erfüllt sein, was sich natürlich sofort zu |
|||||||||||||||||||||||||
| Beziehung für die Schnittweiten s und s' bei einer kugelförmigen Grenzfläche. |
(n1 / s) + (n2 / s') = (n2 - n1) / R
|
||||||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
vereinfachen läßt.
Damit haben wir das 'Klassenziel' erreicht und können einige Spezialfälle diskutieren. Zu diesem Zweck soll die letzte Gleichung noch weiter vereinfacht werden: Den Brechungsindex n1 setzen wir gleich '1' (Vakuum bzw. Luft) und für n2 schreiben wir einfach n. Dann ergibt sich: |
||||||||||||||||||||||||
|
(1 / s) + (n / s') = (n-1) / R
|
|||||||||||||||||||||||||
| ACHTUNG: NÄHERUNG !!! Die Bildweite, - d.h. der Abstand des Punktes D vom Scheitelpunkt B -, wird mit der Strecke s' gleichgesetzt. |
Je weiter der (Quell-)Punkt von der Kugelfläche wegrückt (d.h. je größer die Strecke s wird) , um so dichter rückt der (Bild-)Punkt an die Kugelfläche heran, bzw. s' wird kleiner. | ||||||||||||||||||||||||
| Interessant ist der Fall, wenn der Gegenstandspunkt sehr weit entfernt liegt - wir 'Optiker' reden dann von einem 'unendlich' weit entfernten Quellpunkt - was in der obigen Gleichung durch einen 'unendlich' großen Wert für s beschrieben wird.
In diesem Fall ist (1/s) = 0 Den Abstand des Bildpunktes s', der sich für diesen Grenzfall ergibt, nennt mann die Brennweite f'. Für die Brennweite einer Kugelfläche kann man also schreiben: |
|||||||||||||||||||||||||
| Brennweite einer Kugelfläche: (Brennpunkt in der Kugel) |
f' = n.R / (n-1) |
||||||||||||||||||||||||
|
Da sich der Strahlengang natürlich auch umkehren läßt, hat die Kugelfläche natürlich auch auf der anderen Seite eine Brennweite f. (s' = unendlich und s = f ) : |
|||||||||||||||||||||||||
| Brennweite einer Kugelfläche: (Brennpunkt ausserhalb der Kugel) |
f = R / (n-1)
|
||||||||||||||||||||||||
| Mit dieser Schreibeweise für die Brennweite f kann man die obige Beziehung für die Schnittweiten s und s' in eine etwas bequemere Form bringen: | |||||||||||||||||||||||||
|
1 / s + n / s' = 1 / f
|
|||||||||||||||||||||||||
|
Negative Bildweite !
|
Wir sollten diese Beziehung noch etwas näher betrachten. Was passiert z.B., wenn die Gegenstandsweite s kleiner als die Brennweite f ist, also z.B. s = f/2 ? Dann ergibt sich für s' :
s' = - n . f d.h., die Bildweite s' wird negativ ! Was soll das denn bedeuten ? |
||||||||||||||||||||||||
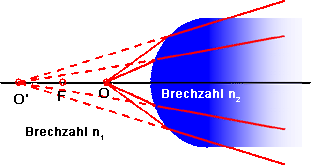
| Der Gegenstandspunkt O befindet sich zwischen dem Brennpunkt F und der Oberfläche. Die Strahlen des Gegenstandspunktes treffen auf die Kugeloberfläche, werden dort gebrochen, aber sie verlaufen weiterhin divergent. Für den Betrachter auf der rechten Seite (also für den Fisch im Kugelaquarium !) scheinen die Lichtstrahlen aus dem virtuellen Bildpunkt O' zu kommen. Die negative Bildweite s' bezieht sich also auf ein scheinbares -virtuelles - Bild. | |||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
|
Abildung mit negativer Bildweite (virtuelles Bild)
|
|||||||||||||||||||||||||
| Im folgenden interaktiven Bildschirmexperiment können wir uns diesen Fall etwas näher betrachten. Verschieben Sie den Gegenstandspunkt O versuchsweise nach rechts, - in Richtung Kugelfläche. Sie können beobachten, wie der Bildpunkt O' ebenfalls nach rechts wandert.
Wenn Sie dicht genug an die Kugelfläche heranfahren, dann können Sie erreichen, dass der Bildpunkt O' rechts im Unendlichen verschwindet und links wieder auftaucht. Das ist genau die Situation, die wir oben diskutiert hatten: Die Gegenstandsweite ist kleiner als die Brennweite geworden ! Übrigens - wenn Sie die Gegenstandsweite nach links so gross wie möglich einstellen, dann rückt der Bildpunkt immer dichter an den Brennpunkt heran. (Für eine unendlich grosse Geghensandsweite, ist der Bildpunkt identisch mit den Brennpunkt. |
|||||||||||||||||||||||||
| Klicken Sie mit der linken Maustaste auf den Gegenstandspunkt. Verschieben Sie den Gegenstandspunkt mit gedrückter Maustaste.
Achtung: Es handelt sich hier nur eine sehr grobe Demonstration der Lichtbrechung an einer Kugelfläche. Bitte schauen Sie nicht zu genau hin, oder messen gar nach ! Achtung: wenn Sie den Gegenstandspunkt aus der Bildfläche herausschieben und die Maustaste loslassen, dann ist er für weitere Manipulationen verloren. Sie müssen diese Seite dann neu aufrufen. |
|
||||||||||||||||||||||||
| Dies ist vielleicht die richtige Stelle, um einige Vereinbarungen über die Vorzeichen der Strecken zu treffen, die bei Linsen(systemen) häufig auftreten; in der folgenden Tabelle sind sie aufgelistet: | |||||||||||||||||||||||||
 |
|
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |