|
PI X E L - Z O O |
|
|
|
11.0 Fata Morgana - die Grenzen des Fermat'schen Prinzips |
| Was hat der Sonnenuntergang eigentlich mit Herrn Fermat zu tun ? | |
|
|
|
| In diesem Kapiel wollen wir 'mal so richtig aufräumen, ergänzen und klarstellen, was bis bislang so im Halschatten bzw. in der Halbwahrheit stand. | |
| Sie kennen solche Bilder! Aber sind Sie auch sicher, dass dieses Bild keine optischeTäuschung ist ? | |
 |
|
|
|
|
|
Als erstes will ich Ihnen das Bild von dem Mann nachreichen , der uns die Grundlage für unsere Überlegungen geliefert hat. Darf ich vorstellen: Pierre de Fermat, geboren 1608 (vielleicht auch 1601)) in Beaumont de Lomagne , |
|
|
Fermat war übrigens "gelernter" Jurist und hat Zeit seines Lebens als Anwalt und später als Richter gearbeitet. Mathematik und Naturwissenschaft war wohl eher ein Hobby, das er im wesentlichen in der ersten Hälfte seines Lebens betrieb. Als einflussreiches Parlamentsmitglied und als Richter hatte er im späteren Leben wohl kaum noch Zeit für solche "Spielereien". Details zum Leben und den Arbeiten von Fermat finden Sie bei Wikipedia. |
 
Pierre de Fermat (1608 - 1665) |
|
|
|
|
So, jetzt zur Sache - ein Sonnenuntergang soll uns weiterhelfen; aber der Reihe nach !
|
|
|
Bitte erinnern Sie sich : Im Kapitel 3 über die Brechung hatten wir uns der 'Behauptung' von Pierre de Fermat angeschlossen, daß ein Lichtstrahl bestrebt ist, den Weg zwischen zwei Punkten in der kürzest möglichen Zeit (nicht auf dem kürzest möglichen Weg !) zurückzulegen. (Am besten Sie schauen sich das noch einmal an - hier klicken!) |
|
|
Aus diesem Prinzip ließ sich sehr elegant das Brechungsgesetz und in der weiteren Folge die Abbildung durch Linsen und Linsensysteme herleiten. Wir hatten auch bereits angedeutet, daß sich das Reflexionsgesetz sehr gut mit dem Fermat'schen Prinzip verträgt, und es wird Sie sicher nicht wundern, daß auch der Strahlverlauf und die Abbildung an Hohlspiegeln sehr einfach mit Hilfe dieses Prinzips zu beschreiben ist, - ist ja im Grunde auch nichts anderes als Reflexion.
|
|
|
Optik - eine Wissenschaft der Grenzflächen ?
|
Bei den bisherigen Betrachtungen war immer eine Grenzfläche im Spiel: z.B. Luft-Wasser, oder Luft-Glas.
An diesen Grenzflächen wird die Ausbreitung des Lichtstrahls beeinflußt; er wird gebrochen und / oder reflektiert, und wenn man diese Grenzflächen geschickt gestaltet, dann lassen sich damit Abbildungen erzeugen. Vor dem Hintergrund dieser Effekte könnte man sich sogar zu der Formulierung hinreißen lassen, daß die Optik die "Wissenschaft der Grenzflächen" ist. |
|
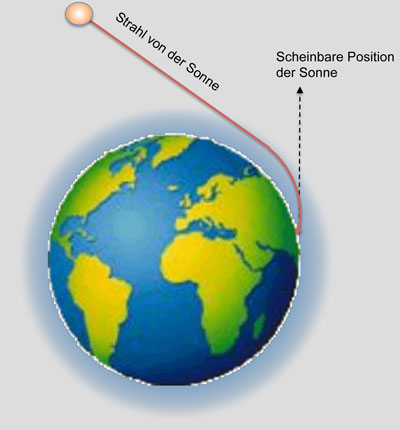
Die letzte Aussage ist mit Vorsicht zu genießen, denn es gibt auch Möglichkeiten, den Verlauf eines Lichtstrahls ohne eine scharf lokalisierte Grenzfläche zu beeinflussen, z.B. wenn sich der Brechungsindex, - d.h. die Ausbreitungsgeschwindigkeit des Lichtes innerhalb eines Mediums -, kontinuierlich ändert. Wenn Fermat mit seinem Prinzip recht hat, dann muß der Lichtstrahl in dieser Situation auf einer gekrümmten Bahn verlaufen. Ein wichtiges Beispiel dafür ist die Ausbreitung des Lichtes in der Athmosphäre: der Luftdruck nimmt von der Erdoberfläche bis in den Weltraum hinein kontinuierlich ab. (Wetterbedingte Luftdruckschwankungen lassen wir mal beiseite!) Da der Brechungindex der Luft eine Funktion der Dichte und damit abhängig vom Luftdruck ist, ändert sich damit auch der Brechungsindex kontinuierlich von einem Wert von etwa 1,000276 (auf der Erdoberfläche) bis auf 1,0 im Vakuum des Weltraumes. |
|
| Sie nehmen die Proportionen dieser Zeichnung bitte nicht wörtlich, - die Atmosphärenhülle ist im Verhältnis zum Erddurchmesser in Wirklichkeit viel dünner unmd auch die Strahlablenkung ist natürlich nicht so stark.
Es geht hier um's Prinzip ! Ach - noch etwas: Da die Krümmung des Lichtstrahls mit abnehmender Winkelhöhe zunimmt, erscheint die Sonnenscheibe am Horizont etwas abgeplattet. Der vertikale Durchmesser wird scheinbar um 6" verkleinert ! (Zitat aus Bergmann-Schaefer, "Lehrbuch der Experimentalphysik", Bd.III, Optik, 1974, Seite 175) |
 |
| Entschuldigung: die Formulierung ".... er wird versuchen einen möglichst großen Teil seines Weges ..." ist natürlich blanker Blödsinn !
Der Lichtstrahl wird gar nichts "versuchen", er gehorcht lediglich einem Naturgesetz. Übrigens: auch der von mir sehr verehrte Richard Feynman ist sich nicht zu schade dem physikalischen Phänomenen menschliches Verhalten zu unterstellen. Er schreibt: ".. und das Licht entscheidet, welches die kürzeste Zeit oder die extreme Zeit ist und wählt diesen Weg. Aber was tut es, wie findet es dies heraus? Riecht es die nahegelegenen Wege und vergleicht diese miteinander? Die Antwort ist, ja, das tut es sozusagen. .... " Achten Sie mal darauf: Sie werden in der naturwissenschaftlich / technischen Literatur immer wieder Formulierungen finden, die der unbelebten Natur eine gewisse Intelligenz oder Eigeninitiative mit durchaus menschlichen Verhaltensweisen zutraut. - Vielleicht ein interessantes Phänomen für einen Psychologen? |
Wenn ein Lichtstrahl von der tiefstehenden Abendsonne schräg auf die Lufthülle der Erde trifft, dann wird er versuchen, einen möglichst großen Teil seines Weges in den Luftschichten mit kleinem Brechungsindex, d.h. hoher Geschwindigkeit und einen möglichst kurzen Teil in den Bereichen mit großem Brechungsindex zurückzulegen. Daraus resultiert der im obigen Bild dargestellte, gebogene Strahlverlauf.
Wenn wir die Sonne am Abend noch über dem Horizont sehen, befindet sie sich in Wahrheit schon längst darunter !
|
|
Um eine ganz ähnliche Erscheinung handelt es sich bei der Fata Morgana, einer Luftspiegelung über einer heißen Oberfläche, z.B. einer Straße oder dem heißen Wüstensand. Durch die hohen Temperaturen in der Nähe der Straße entsteht eine Verteilung des Brechungsindex, die dafür sorgt, daß der Lichtstrahl auf einer nach oben gekrümmten Bahn verläuft, weil dieser zeitlich kürzer ist als der direkte. Im Bild unten wird die Palme gespiegelt; sehr viel öfter können Sie aber die Spiegelung des Himmels beobachten, was dann wie eine große blaue, durch den Einfluß der Luftschlieren wellige Fläche aussieht und dem Verdurstenden in der Wüste wie ein Gewässer vorgaukelt.
|
|
|
Diese Beispiele für die Ausbreitung des Lichtes in einem Medium, dessen Brechungsindex sich kontinuierlich ändert, machen deutlich, daß wir das Fermat'sche Prinzip doch noch etwas genauer definieren müssen.
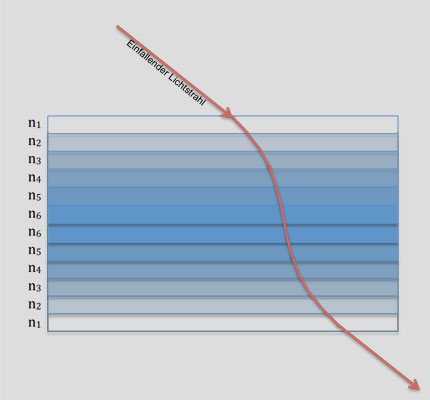
Um den Übergang zu einer kontinuierlichen Schichtung des Brechungsindex in den Griff zu bekommen, starten wir zunächst mit einem Beispiel, bei dem der Lichstrahl durch einen Glasplattenstapel aus den unterschiedlichsten Glassorten hindurchläuft: |
|
| Ein nette Denksportaufgabe:
Auf beiden Seiten des Plattenstapels befindet sich dasselbe Medium, d.h., gleicher Brechungsindex. Für die Platten des Stapels sei jeder beliebige Brechungsindex und jede beliebige Verteilung zugelassen. Wie sind der austretende und der einfallende Lichtstrahl zueinander angeordnet? (Das Ergebnis finden Sie hier.) |
 |
|
Wenn Sie den ganzen "Formelkram" nicht mögen, dann lesen Sie jetzt bitte hier auf der linken Seite weiter - Sie verpassen nichts - na,ja, - fast nichts ! |
Durch eine geeignete Staffelung der Brechungsindices läßt sich fast jeder Strahlverlauf einstellen. Aber natürlich gilt auch hier Fermats Forderung, daß die Gesamtzeit ein Minimum sein sollte. Wenn man die Teilwegstrecken in den Glasplatten mit si und die jeweiligen Geschwindigkeiten des Lichtes mit vi bezeichnet, dann gilt für die gesamte Laufzeit
|
|
Wir bilden die Summe der Laufzeiten für die einzelnen Teilstrecken in dem oben gezeigten Glasplattenstapel und .....
|
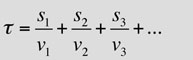 oder: |
|
|
|
|
Nun kann man, wie Sie sich bestimmt erinnern, die Lichtgeschwindigkeit vi innerhalb eines bestimmten Mediums durch den Brechungsindex ni und die Vakuumlichtgeschwindigkeit co ausdrücken :
|
|
|
d.h. der obige Summenausdruck für die Laufzeit
|
|
|
.....rechnen diesen Wert in die optische Weglänge um. Achtung nicht verwechseln - Wir reden hier nicht von der geometrischen Weglänge, sondern von der optischen Weglänge und die ergibt sich aus dem Produkt von Brechungsindex und der geometrischen Wegstrecke und ist damit ein Maß für die Laufzeitt (Gehen Sie doch 'mal zurück zu Kapitel 3 wo wir uns über die "optische Weglänge" untgerhalten haben !) |
Das Produkt ni . si ist die sog. 'optische Weglänge'. Man kann das Fermat'sche Prinzip deshalb auch umformulieren :
|
|
Nach dem Fermat'schen Prinzip gilt, dass das Licht die Strecke zwischen zwei Punkten in der kürzestest möglichen Zeit, d.h. auf der kleinsten optischen Weglänge durchläuft. |
"Das Licht durchläuft eine Strecke zwischen zwei Punkten auf der kleinsten optischen Weglänge." |
| Jetzt stellen Sie sich bitte vor, dass die Schichten in dem Glasstapel oben immer dünner werden und die Änderung des Brechungsindex von Schicht zu Schicht immer kleiner, so daß wir schließlich zu einer ganz gleichmäßigen Änderung des Brechungsindex gelangen, - so wie oben für die Lufthülle rund um die Erde beschrieben - dann verläuft der LIchtstrahl auf einer gleichmäßig gekrümmten Bahn. |
Für ein Medium mit kontinuierlicher Verteilung des Brechungsindex muß die Summe allerdings durch ein Integral ersetzt werden:
|
|
oder, wenn man sich auf die optische Weglänge L konzentriert:
|
|
|
|
|
|
Achtung - neuer Gesichtspunkt !
Bevor wir diesen Formalismus weiter entwickeln, sollten wir uns innerlich zurücklehnen und überlegen, was wir hier eigentlich treiben! |
|
| Möglicherweise geht es Ihnen so wie mir : Irgendwie hat man das Gefühl, das diese Prinzipien mit der kürzesten Zeit (Fermat) oder dem kürzesten Weg (Hero) noch nicht ganz den Kern der Wahrheit treffen.
Vielleicht hatten Sie bereits bei der Diskussion um die Reflexion an einer Spiegeloberfläche den Eindruck, daß hier etwas nicht stimmen kann. Schauen Sie doch noch einmal ins Kapitel 2 : Der Lichtstrahl, der in der kürzesten Zeit - und auf dem kürzesten Weg - vom Startpunkt zum Endpunkt gelangt, ist natürlich der direkte und nicht derjenige, der den Umweg über die Spiegeloberfläche nimmt ! Um Sie nicht auf diesen Gedanken zu bringen, hatte ich diese direkte Verbindung in den Bildern gar nicht erst eingezeichnet. |
|
| Was ist also dran an einem Prinzip, das es offensichtlich gestattet, die Gesetze der Lichtausbreitung richtig herzuleiten, obwohl es eigentlich falsch ist ?
Antwort: Wir haben uns bisher mit einer Halbwahrheit begnügt und - halb wahr ist eben auch falsch ! |
|
|
|
|
|
Die richtigere Formulierung, die die von uns bisher benutzte mit einschließt, lautet: |
|
| "Ein Lichtstrahl muß beim Durchgang vom Startpunkt zum Endpunkt eine optische Weglänge durchlaufen, die stationär in bezug auf Änderungen jenes Weges ist." Zitat aus E.Hecht, "Optik", Addison-Wesley Publishing Comp. 1989, Seite 96. |
Die Angelegenheit läßt sich (natürlich !) auch etwas mathematischer formulieren: Um den Extremwert der Laufzeit
|
| oder etwas konkreter: |
und zur Herleitung des Brechungsgesetzes auf den Ausdruck für die Laufzeit angewandt. (Hier geht's noch einmal zurück zu Kapitel 3.)
|
| "Ein Strahl, der sich auf einem bestimmten speziellen Weg bewegt, hat die Eigenschaft, daß es bei kleinen Änderungen (sagen wir einer einprozentigen Verschiebung) des Strahles in einer x-beliebigen Weise, sagen wir des Ortes, wo er auf den Spiegel trifft, oder der Kurvenform oder sonst irgend etwas, in erster Näherung keine Zeitänderung gibt." Zitat aus: Richard P. Feynman, "Vorlesungen über Physik", Bd.1, Oldenbourg Verlag, 1991, Seite 363 oben. |
|
|
Wir hatten oben für die gesamte optische Weglänge den Ausdruck |
|
|
|
|
|
notiert. Wenn
|
|
|
d.h., die Variation mit des optischen Weges ist Null.
.... und diese Bedingung wird eben bei der Fata Morgana oder beim Sonnenuntergang für die gekrümmten Lichtstrahlen am besten erfüllt ! |
|
 |
Sie werden einwenden, dass diese Art der Optimierung des Strahlverlaufes nicht mehr viel mit Fermats Kriterium der kürzesten Zeit zu tun hat !
Ja und Nein - wenn Sie nämlich aus der Vielzahl der möglichen Strahlverläufe denjenigen mit der kürzesten Zeit heraussuchen, also das Minimum, dann sind im Normalfall (einen stetigen Funktiionsverlauf vorausgesetzt) die Laufzeiten der benachbarbarten Strahlverläufe sehr ähnlich, d.h. die Variation des ist annähernd Null. |
|
|
Mit dieser letzten Formulierung des Fermat'schen Prinzips ist den Formalisten hoffentlich Genüge getan, und wir können uns der Frage zuwenden was denn die physikalische Bedeutung dieses so umformulierten Fermat'schen Prinzips sein könnte.
|
|
Also - um was geht es hier eigentlich ?
|
|
| Der Lichtstrahl verläuft offenbar bevorzugt auf den Wegstrecken, bei denen gerinfügige Verschiebungen keine große Auswirkung auf die Laufzeit haben. Ein dicht benachbarter Strahl trifft deshalb annähernd zur gleichen Zeit, d.h. mit der gleichen Phasenlage, am Zielort ein. |
Wenn wir mal für einen kurzen Momemt die Strahlenoptik vergessen und uns daran erinnern, daß man das Licht auch als Welle beschreiben kann, dann wird sofort klar, was hinter dem Variationsprinzip des optischen Weges steckt:
Gleiche Phasenlage zwischen benachbarten Lichtstrahlen bedeutet konstruktive Interferenz, d.h. durch die Überlagerung der Strahlen am Bildort werden sie sich gegenseitig verstärken. Diejenigen optischen Wege, bei denen diese Randbedingung erfüllt ist, tragen zur Entstehung eines Bildes bei, diejenigen bei denen diese Bedingung nicht erfüllt ist sind uninteressant, weil sich die benachbarten Strahlen am Bildort auslöschen. |
|
Das ist natürlich ein herbe Enttäuschung für diejenigen von Ihnen, die im Fermat'schen Prinzip den Ausdruck eines ordnenden Prinzips sehen wollen, im Sinne eines göttlichen Lenkers, der jedem Lichtstrahl kurz bevor er die Quelle verläßt zuflüstert, welches wohl der kürzeste bzw. beste Weg zum Ziel sein könnte. Nein, - ich fürchte die Angelegenheit ist viel profaner : |
Ob benachbarte Strahlen zur Bildentstehung beitragen können, wird durch das "Eikonal" beschrieben , benannt nach dem griechischen Wort "
|
|
Eine Lichtquelle sendet ihre Strahlen ganz wahl- und ziellos aus; einige davon bleiben erhalten und gelagen an ein Ziel, andere löschen sich gegenseitig durch Überlagerung aus. Das ist alles ! ... und wenn man es schlau anstellt, - z.B. mit geeignet geformten Gläsern (=Linsen) - dann formen die "überlebenden" Lichtstrahlen ein Bild ! |
Mit einem übergeordneten Lenker und Planer, der in die Abläufe der Natur steuernd eingreift, mit dem Ziel, irgendeine Art von Optimierung zu erreichen, hat das wenig zu tun, - zumindest was den Weg eines Lichtstrahls betrifft ! |
|
|
|
|
Zum Abschluß dieses Kapitels soll noch ein Gedanke von Feynman vorgestellt werden, wonach das Fermat'sche Prinzip sogar als Erklärungsgrundlage für die Beugung des Lichtes dienen kann.
|
|
|
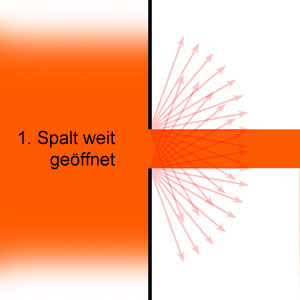
In den folgenden Skizzen ist eine Blende (schwarzer senkrechter Balken) dargestellt, die von einem ausgedehnten Lichtstrahl von links getroffen wird.
|
|
|
|
|
|
Wenn der Spalt weit geöffnet ist tritt ein breiter Lichtstrom hindurch und dahinter würde ein Detektor im Bereich des Spaltes ein bestimmte Strahlungsintensität messen können, außerhalb dieses beleuchteten Bereichs wäre der Detektor im Schatten der Blende, - die gemessene Strahlungsintensität ist annähernd Null.
|
|
|
|
Ja ja, ich gebe es zu: eine ziemlich umständliche Beschreibung des Schattenwurfes einer Blende !
Aber der spannende Teil der Geschichte kommt jetzt: |
 |
An den Kanten der geöffneten Blende entsteht ein kleiner Anteil an Streulicht, was die Ränder des hindurchtretenden Lichtbandes etwas unscharf macht, im übrigen aber keine große Auswirkung hat.
Das Streulicht vagabundiert kreuz und quer und verliert sich im Raum - die Laufwege der gestreuten Lichtstrahlen sind so unterschiedlich, dass keine konstruktive Überlagerung entstehen kann. |
|
Mit unserem neu gewonnenen Wissen würden wir sagen das Eikonal ist ungleich Null ! (s.o.) |
|
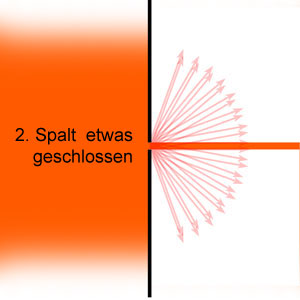 |
Wenn wir den Spalt weiter schliessen, dann rücken auch die Streulichtkegel dichter aneinander, aber für eine konstruktive Überlagereung (Interferenz) reicht das noch nicht ganz:
|
|
|
|
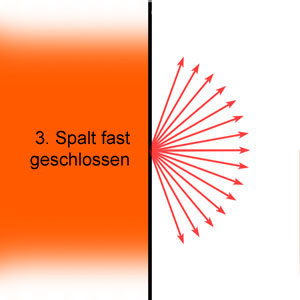 |
Erst wenn wir den Spalt fast schliessen - konkret heisst das: die Spaltöffnung ist kleiner als die Wellenlänge - dann liegen die Streulichtkegel so dicht beieinander, dass sie sich (annähernd phasenrichtig) überlagern und damit gegenseitig verstärken können. Jetzt ist der Raum hinter der Blende zwar sehr schwach, aber einigermassen gleichmässig ausgeleuchtet, - wir haben Beugung ! (Das Eikonal ist annähernd Null!)
|
| Na gut - das war jetzt eine stark vereinfachte Darstellung, um Ihnen das Prinzip zu verdeutlichen:
In der Praxis sollten Sie dieses Experiment nicht mit Licht sondern mit Mikro- bzw. cm-Wellen durchführen, um einen deutlichen Effekt zu sehen. (Bei den kleinen Lichtwellenlängen - ca 0,0005 mm müssten Sie den Spalt schon verdammt weit zudrehen um diesen gleichmäßigen Beugungseffekt zu sehen.) Und noch etwas, was in den Skizzen oben nicht richtig zum Ausdruck kommt: |
 |
|
|
Wir haben damit auf der Basis des Fermat'schen Prinzips einen Effekt erklärt, der eigentlich erst mit den Mitteln der Wellenoptik vollständig beschrieben werden kann.
Hätten Sie gedacht, daß das Fermat'sche Prinzip soweit reicht ? |
|
|
|
|
|
|
| . |
|
