|
PI X E L - Z O O |
|||||||||||||||||||||
|
8. Abbildungen |
|||||||||||||||||||||
|
|
|||||||||||||||||||||
|
"Optische Achse" = zentrale Linie auf der alle Komponenten aufgereiht sind. |
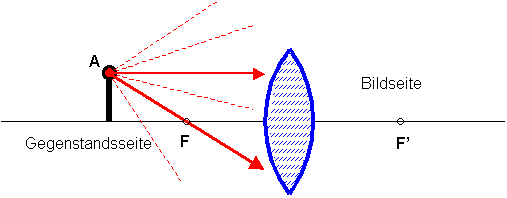
Bis hierher haben wir immer nur Bild- und Gegenstandspunkte auf der 'optischen Achse' betrachtet. Das ist relativ uninteressant - welches Bild besteht nur aus einem Punkt ? Wir müssen uns nun der Frage zuwenden, wie Gegenstandspunkte abgebildet werden, die außerhalb der optischen Achse liegen. Im folgenden Bild ist die Ausgangssituation skizziert. Vorgegeben ist eine (bikonvexe) Linse und die Lage ihrer Brennpunkte F und F'. Von einem außeraxialen Gegenstandspunkt A startet ein divergentes Strahlenbündel. Nun ist die Frage zu beantworten auf welchem (Bild-)Punkt wird dieses Strahlenbündel fokussiert? |
||||||||||||||||||||
 |
|||||||||||||||||||||
|
|
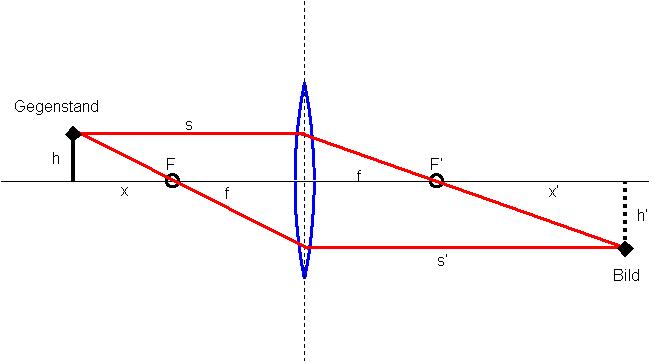
Nun, für einen beliebigen einzelnen Strahl ist diese Frage gar nicht so leicht zu beantworten. Man müßte ihn unter Anwendung des Brechungsgesetzes durch die Linse verfolgen, um seine Position und Richtung auf der Bildseite der Linse festlegen zu können. Die ganze Angelegenheit läßt sich jedoch erheblich vereinfachen: Für ganz bestimmte Strahlen auf der Gegenstandsseite kennen wir nämlich bereits den vollständigen Strahlverlauf. Dazu müssen wir nur die beiden Regeln aus Kapitel 7 "Dünne Linsen" Abschnitt anwenden: Der Strahl, der parallel zur optischen Achse einfällt, wird auf der Bildseite durch den Brennpunkt F' gelenkt, - und der Strahl, der auf der Gegenstandsseite durch den Brennpunkt F verläuft, verläßt die Linse auf der Bildseite parallel zur optischen Achse. Dort, wo sich die beiden Strahlen treffen, befindet sich der Bildpunkt. Die Skizze im folgenden Bild zeigt die Einzelheiten. Im Interaktive Bildschirm Experiment (IBE) im Kapitel 7 hatten wir uns bereits angesehen, wie sich der Strahlverlauf durch Verschieben des Gegestandes verändert, - blättern Sie noch einmal zurück und schauen Sie sich das noch einmal an ! |
||||||||||||||||||||
| Die Linse ist durch einen einzigen senkrechten Strich dargestellt, - daher der Name 'dünne Linse' ! |
|
||||||||||||||||||||
|
s = x + f und für die Bildweite s' gilt: s' = x' + f. |
|||||||||||||||||||||
|
Setzen wir dies in die Linsengleichung (1/s + 1/s' = 1/f ) ein, dann erhält man: |
|||||||||||||||||||||
|
Newton'sche Abbildungs gleichung |
x'.x = f2
|
||||||||||||||||||||
|
wobei x und x' die jeweiligen Abstände zum Brennpunkt sind. Wenn also z.B. der Gegenstand sich im Brennpunkt befindet, d.h. x = 0, dann befindet sich das Bild ( x' = f2 / x) im 'Unendlichen', - was das auch immer heißen mag ! |
|||||||||||||||||||||
|
Laterale Vergrößerung = Abbildungsmaßstab = Transversalvergrößerung! Die Autoren der verschiedenen Lehrbücher können sich leider nicht auf einen einheitlichen Begriff einigen. Ganz wichtig ist die folgende Festlegung: Wenn die Vergrößerung negativ angegeben wird, dann ist der Gegenstand aufrecht (h positiv) und das Bild umgekehrt (h' negativ). |
Mit Hilfe des 'Strahlensatzes' lassen sich aus dem obigen Bild die folgenden Zusammenhänge ablesen: h' / f = h / x Daraus ergibt sich die (laterale) Vergrößerung vL = h' / h zu: vL = h' / h = f / x Je dichter der Gegenstand an den Brennpunkt heranrückt ( d.h. x --> 0 ) um so größer wird das Bild. Wenn Sie Newton'sche Gleichung zu Rate ziehen, dann stellen Sie fest, daß dieses unendlich große Bild auch unendlich weit entfernt ist. |
||||||||||||||||||||
|
Bitte verfallen Sie jetzt nicht dem Irrglauben, wir hätten jetzt das Problem der Vergrößerung von optischen Systemen im Griff. Neben der 'Lateralvergrößerung' gibt es noch den - vielleicht viel wichtigeren - Begriff der 'Winkelvergrößerung',. Bei einem Fernrohr z.B. ist die laterale Größe des Bildes auf der Netzhaut des Beobachters in aller Regel sehr viel kleiner als der Gegenstand (z.B. ein Kirchturm !) selbst. Aber der Blickwinkel (=Öffnungswinkel zwischen dem Kirchturmfuß und der Kirchturmspitze) unter dem der Gegenstand bei Betrachtung durch das Fernrohr erscheint hat sich vergrößert. Aber darüber unterhalten wir uns an anderer Stelle ! |
|||||||||||||||||||||
| So, - damit Sie nicht ständig hin und her springen müssen um die Abbildung durch eine dünne Linse zu simulieren, habe ich für Sie das interaktive Bildschirm-Experriment (IBE) vom letzten Kapitel 7 hier noch einmal installiert. Und so funktioniert es :
Im folgenden Bild stellt der blaue Pfeil auf der linken Seite den abzubildenden "Gegenstand" dar. Der dünne schwarze Pfeil auf der rechten Seite ist das "Bild". Klicken Sie bitte mit der linken Maustaste auf die Spitze des "Gegenstandes" (blauer Pfeil) und bewegen Sie die Maus mit gedrückter linker Taste. Auf diese Weise können Sie die Größe und die Position des "Gegenstandes" verändern. Beobachten Sie bitte, wie sich das "Bild" in Abhängigkeit von der Position des "Gegenstandes" verändert. |
|||||||||||||||||||||
| Interaktives Bildschirmexperiment:
Abbildung durch eine "dünne" Linse. (Bitte seien Sie nachsichtig mit meinen Zeichenkünsten: die "dünne" Linse ist ganz schön dick ausgefallen ! Sie verstehen sicher was gemeint ist: es handelt sich hier nur um ein Symbol.) (Bitte bleiben Sie mit dem "Gegenstand" nur auf der linken Seite der Linse - auf der rechten Seite versagt der Simulationsalgorithmus !) |
|
||||||||||||||||||||
| Abbildung durch eine dünne Linse. | |||||||||||||||||||||
| Hier wichtigsten Ergebnisse unseres (Ihres) Experimentes:
1. Das "Bild" steht immer auf dem Kopf. |
|||||||||||||||||||||
|
2. Wenn sich der "Gegenstand" zwischen den Punkten F (Brennpunkt der Linse) und 2F ( doppelte Brennweite) befindet, dann wird das "Bild" vergrössert. |
|||||||||||||||||||||
| Das können Sie zwar nicht sehen, aber das glauben Sie sicher. Oder ? |
3. Befindet sich der "Gegenstand" genau im Brennpunkt F, dann ist das "Bild" unendlich weit entfernt und unendlich groß. |
||||||||||||||||||||
|
4. Wenn sich der "Gegenstand" im Punkt 2F (doppelte Brennweite) befindet, dann ist das "Bild" genauso groß wie der "Gegenstand" und der Abstand zur Linse ist ebenfalls die doppelte Brennweite (Punkt 2F'). |
|||||||||||||||||||||
|
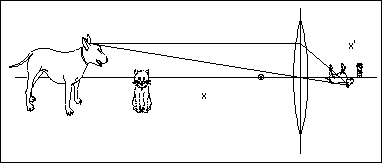
Richtig interessant wir die Sache aber erst, wenn wir die Tiefenausdehnung eines Gegenstandes mit ins Kalkül ziehen. Im folgenden Bild sitzen Hund und Katze in unterschiedlicher Entfernung vor der abbildenden Linse. Wenn Sie nun mit den bisher ver-wendeten Rezepten die Abbildung der beiden konstruieren, dann werden Sie feststellen, daß sich auf der Bildseite der Hund näher an der Linsen befindet als die Katze - auf der Gegenstandsseite ist es umgekehrt. (Ausserdem ist die Katze auf der Bildseite grösser und der Hund kleiner - was der Katze sicher Mut macht ! Ausserdem stehen beide Kopf !) |
|||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
|
||||||||||||||||||||
|
Etwas mathematischer ausgedrückt: Sie lösen die Newton'sche Gleichung nach x' auf und differenzieren nach x ! Ganz einfach, - nicht ? |
Der Tiefenmaßstab vt, - d.h. die Änderung der Bildtiefe dx' in Abhängigkeit von der Änderung der Gegenstandstiefe dx und der Gegenstandsweite x -, läßt sich formal sehr einfach aus der Newton'schen Abbildungsgleichung herleiten.
|
||||||||||||||||||||
|
vt = dx' / dx = - f2 / x2
|
|||||||||||||||||||||
|
d.h. das Tiefenverhältnis ist grundsätzlich negativ, was nach den Vorzeichenkonventionen für optische Abbildungen bedeutet, daß z.B. ein ausgestreckter Zeigefinger, der auf der Gegenstandsseite in die Richtung der Linse deutet, auf der Bildseite von ihr weg zeigt.
|
|||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Für die weitere Behandlung von Abbildungen - z.B. durch eine Gruppe von Linsen - müssen wir noch eine andere Frage beantworten: Was machen Sie, wenn Sie den Verlauf eines unter beliebigem Einfallswinkel auf die Linse auftreffenden Strahls verfolgen wollen ? Der Lichtstrahl tut Ihnen leider nur ganz selten den Gefallen, entweder durch den Brennpunkt oder parallel zur optischen Achse zu verlaufen, so daß Sie die Regeln von Seite 26 verwenden können. |
||||||||||||||||||||
| Eigentlich ist die 'Brennebene' keine Ebene, sondern ebenfalls eine Kugelfläche, da wir uns aber auf Paraxialstrahlen - also Strahlen die in der Nähe der optischen Achse verlaufen - beschränken, kann man die 'Brennsphäre' auch als 'Brennebene 'betrachten. |
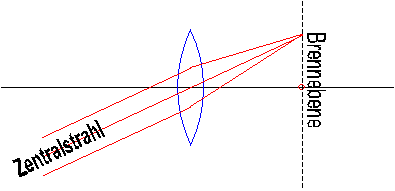
Hier das 'Rezept': Ausgangspunkt der Überlegung ist die Behauptung, daß ein paralleles Strahlenbündel immer im Brennpunkt - bzw. in der Brennebene der Linse gesammelt wird. Ein Strahlenbündel, das genau in Richtung der optischen Achse auf die Linse auftrifft, wird in einem Brennpunkt fokussiert, der auf der optischen Achse liegt. (Regel 1 in Kapitel 7)) Ein schräg auftreffendes Strahlenbündel wird natürlich ebenfalls fokussiert, aber auf einen Brennpunkt außerhalb der optischen Achse, so, wie in der folgenden Skizze dargestellt. |
||||||||||||||||||||
 |
|||||||||||||||||||||
| Um die Position des Brennpunktes zu ermitteln, geht man nun folgendermaßen vor: Der Zentralstrahl des Strahlenbündels durchläuft die (Dünne-) Linse unverändert und kreuzt die Brennebene genau an der Stelle, an der auch die übrigen Teilstrahlen eintreffen. Damit ist der Brennpunkt für dieses Bündel bestimmt. Mit Hilfe dieser Überlegung läßt sich nun auch der Verlauf eines beliebigen Einzelstrahls durch die Linse verfolgen. Die Konstruktion ist in der folgenden Bilderserie ausführlich erläutert. | |||||||||||||||||||||
 |
|||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
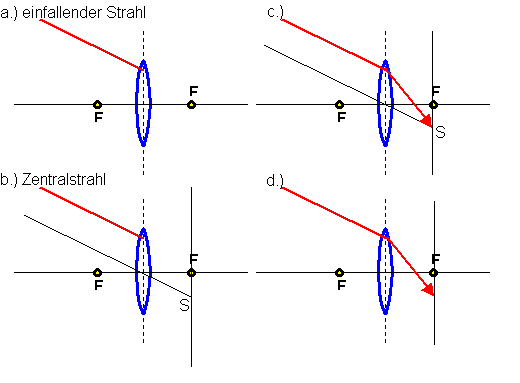
Konstruktion des Strahlverlaufes durch eine dünne Linse für einen beliebigen, schräg einfallenden Strahl.
In Teilbild (a) ist zunächst ein aus einer beliebigen Richtung eintreffender Lichtstrahl dargestellt. Im nächsten Teilbild (b) wird die Parallele zu diesem Strahl durch das Linsenzentrum konstruiert und der Schnittpunkt S mit der bildseitigen Brennebene ermittelt. Da Parallelstrahlen sich grundsätzlich in einem Punkt in der Brennebene treffen, ist damit auch der weitere Verlauf des Strahls festgelegt. (c) und (d) |
||||||||||||||||||||
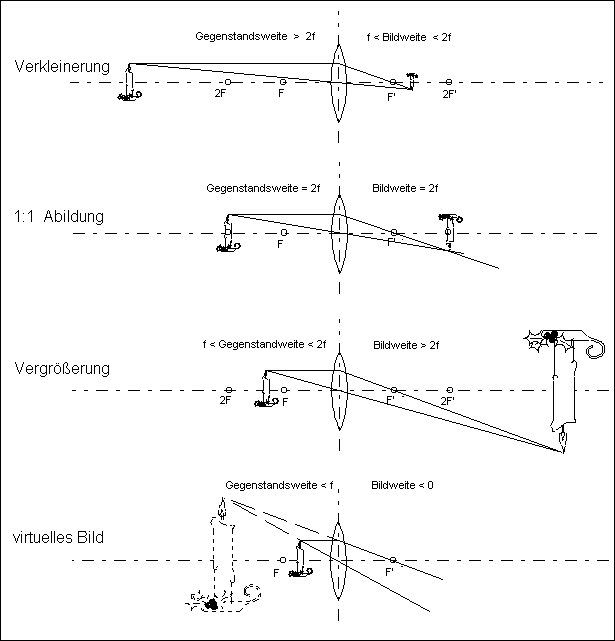
| Bevor wir uns mit den Eigenschaften eines Systems aus dünnen Linsen beschäftigen, wollen wir die wesentlichen Merkmale für die Abbildung durch eine 'dünne' Linse noch einmal zusammenfassen. (Sie sollten die verschiedenen Abbildungssituationen auch noch einmal mit unserem Interaktiven Bildschirm-Experiment "Strahlverlauf durch eine dünne Linse" nachvollziehen) | |||||||||||||||||||||
|
|
|||||||||||||||||||||
| Abbildung durch eine dünne Linse bei verschiedenen Gegenstandsweiten. | |||||||||||||||||||||
| Die Vergrößerung und die Entfernung des Bildes von der abbildenden Linse (Bildweite) hängt direkt von der Gegenstandsweite ab. Wenn der Abstand des Gegenstand zur Linse kleiner als die Brennweite ist, dann entsteht überhaupt kein reelles Bild mehr, sondern nur noch ein virtuelles, zu dessen Betrachtung eine weitere Optik, - z.B. das Auge -, notwendig ist. Zur Vervollständigung dieses Überblicks kann vielleicht die folgende Tabelle dienen: | |||||||||||||||||||||
|
|||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
Bildweite, Vegrößerung und Bildlage einer Konvexlinse in Abhängigkeit von der Gegenstandsweite. | ||||||||||||||||||||
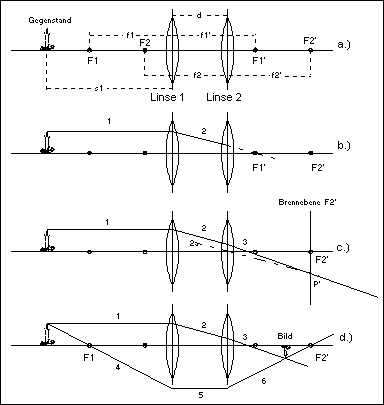
| Mit den bisher vorgestellten Werkzeugen lassen sich nun auch Abbildungen durch beliebig komplexe Linsensysteme konstruieren. In den folgenden Skizzen ist als Beispiel die Abbildung durch zwei dünnen Linsen dargestellt. | |||||||||||||||||||||
 |
|||||||||||||||||||||
| Ein 'reelles' Bild liegt dann vor, wenn man einen Schirm in den Strahlengang halten kann und darauf ein Bild des Gegenstandes entsteht. Bei einem 'vir-tuellen' Bild ist das nicht der Fall. Trotzdem ist ein 'virtuelles' Bild nicht nutzlos, - man muß nur eine weitere Abbildung durchführen, z.B. mit dem Auge, und dann entsteht ein relles Bild auf der Netzhaut. | Abildung durch ein Linsensystem. Abstand der Linsen ist kleiner die Einzelbrennweiten f1 und f2 .
Zwei 'dünne' Linsen mit den Brennweiten f1 und f2 befinden sich in einem Abstand, der kleiner ist als die kleinste Einzelbrennweite (d < f1 , f2) . Zur Konstruktion des Bildes wird vom Gegenstand ein Parallelstrahl ('1') in Richtung auf die Linse 1 gezogen(b). Strahl '1' verläßt die Linse 1 in Richtung Brennpunkt F1' und trifft vorher aber bereits auf Linse 2 (Strahl '2'). Um zu ermitteln, in welcher Weise Strahl '2' von der Linse 2 beeinflußt wird, wird die Parallele zu '2' durch das Zentrum der Linse 2 gezogen. (Gerade '2a' im Teilbild c). Die Gerade '2a' schneidet die Brennebene F2' im Punkt P'. Wenn man nun den Strahl '2' durch den Punkt P' verlängert (Strahl '3'), dann ist der Verlauf dieses Teilstrahls durch das Linsensystem komplett. |
||||||||||||||||||||
| So weit, so gut.
Aber Sie sind jetzt sicher an einer (etwas) praxisnäheren Demonstration interessiert. Ich bin ziemlich stolz, Ihnen im folgenden Interaktiven Blischirm-Experiment die Abbildung , bzw. den Strahlverlauf durch zwei hintereinandergeschaltete dünne Linsen demonstrieren zu können. |
|||||||||||||||||||||
| Klicken Sie bitte mit der linken Maustaste auf die Spitze des "Gegenstandes" und halten Sie die Taste gedrückt. Jetzt können Sie den "Gegenstand" mit der Maus verschieben, - vor und zurück, größer oder kleiner. | |||||||||||||||||||||
| Bei der Darstellung der Linsen durch dicke Striche habe ich mir das Lebens etwas leichter gemacht, - aber ich hoffe, dass Sie trotzdem erkennen können was gemeint ist ! ? | |||||||||||||||||||||
|
|
|||||||||||||||||||||
| Strahlverlauf / Abbildung durch zwei hintereinander geschaltete dünne Linsen.
Das besondere an diesem interaktiven Bildschirm-Experiment ist die Tatsache, dass Sie sämtliche Parameter ändern können: sowohl den Abstand zwischen den Linsen als auch deren Brennweiten. 'Klicken' dazu einfach auf einen der grünen bzw. roten Punkte und verschieben sie ihn mit gedrückter linker Maustaste. Übrigens: Sie können mit dieser Linsenanordnung sehr einfach den Strahlengang eines Mirkoskops oder eines astronomischen Fernrohres simulieren, - aber dazu später mehr ! Im Augenblick sollten Sie einfach 'mal etwas herumspielen. Verändern Sie die Entfernung und die Grösse des Gegenstandes, oder die Brennweiten und den Abstand zwischen den Linsen und beobachten Sie was mit der Abbildung passiert. Versuchen Sie z.B. die folgende Einstellung: Schieben Sie die Linsen ganz dicht zusammen und machen Sie die Brennweiten annähernd gleich gross. Die Abbildung, die sich jetzt ergibt, verhält sich (fast) genauso wie bei einer einzelnen Linsen (s. d. Abbildung durch eine dünne Linse) : das Bild ist reell und steht auf dem Kopf ! Allerdings, der Abstand bei dem sich eine 1:1-Abbildung ergibt, entspricht (in etwa) der Brennweite der Einzellinsen. (Sie erinnern sich? Bei einer einzelnen dünnen Linse war dieser Abstand die doppelte Brennweite.) Daraus kann man schliessen, dass sich die effektive Brennweite der Linsenkombination halbiert hat. - Darauf kommen wir gleich zurück ! |
|||||||||||||||||||||
| Vorsicht jetzt kommt wieder etwas Mathematik, - aber nur ganz wenig (Grunschulniveau !). | Was wir eben an dem Interaktiven Bildschirm-Experiment etwas spielerisch untersucht haben, wollen wir jetzt etwas genauer fassen:
Wo liegt der Brennpunkt dieses Linsensystems ? Also: Nehmen Sie 'mal an, auf unser Linsensystem trifft von links, von der "Gegenstandsseite", ein Bündel paralleler Lichtstrahlen; der Punkt an dem sich diese Lichtstrahlen auf der "Bildseite" des Linsensystems treffen, wäre dann der Brennpunkt des Gesamtsystems. Bevor wir anfangen zu rechnen, sollten wir uns noch einmal die Parameter notieren mit den wir es jetzt gleich zu tun bekommen: s1, s1' - Gegenstands- und Bildweite von Linse 1 Zur Veranschaulichung habe ich das alles in der folgenden Skizze zusammengestellt: |
||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
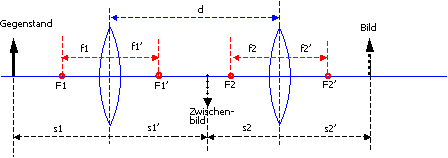 |
||||||||||||||||||||
| Was wir ausserdem brauchen, ist die Linsengleichung aus Kapitel 7:
1/s + 1/s' = 1/f wobei s die Gegenstands- , s' die Bild- und f die Brennweite einer beliebigen Linse ist. Für die zweite LInse lautet die Linsengleichung: 1/s2' = 1/f2 - 1/s2 |
|||||||||||||||||||||
| Bitte beachten Sie die Wortwahl: wir bestimmen hier den Abstand des Systembrennpunktes von der bildseitigen Linse. Das ist nicht dasselbe wie die Systembrennweite !
s1 "gegen unendlich", das bedeutet eine unendlich weit entfernte Lichtquelle, und daraus wiederum folgt, dass es sich bei demn einfallenden Licht um ein paralleles Strahlenbündel handelt. |
Richtig, - den Abstand des effektiven Brennpunktes des Gesamtsystems von der bildseitigen Linse: fsys' Damit Sie bei den folgenden Manipulation nicht den Überblick verlieren sollte ich Ihnen verraten was wir eigentlich vorhaben: wir wollen herausfinden wie sich die Bildweite am Ausgang unseres Linsensystems s2' verändert, wenn die Gegenstandsweite s1 am Eingang gegen "Unendlich" geht. Die Bildweite der zweiten Linse s2' ist identisch mit dem Brennpunktabstand fsys', wenn s1 gegen unendlich geht! fsys' = s2' |
||||||||||||||||||||
| Die Vorzeichenkonventionen für die verschiedenen Abstände finden Sie in Kapitel 7. | So, jetzt wollen wir in der Linsengleichung 1/s2' = 1/f2 - 1/s2 für Linse 2 einige Ersetzungen durchführen.
Aus der obigen Skizze ist sofort zu sehen, dass s2 = d - s1' gilt . Mit Hilfe der Linsengleichung für Linse 1 1/f1 = 1/s1 + 1/s1' kann ausserdem s1' durch die Gegenstandsweite s1 ersetzt werden: 1/s1' = 1/f1 - 1/s1 = (s1 - f1) / (f1.s1) bzw.: s2 = d - s1' = d - (f1.s1) / (s1-f1) Fügt man diesen Ausdruck für die Gegenstandsweite von Linse 2 in die Linsengleichung von Linse 2, ( 1/f2 = 1/s2 + 1/s2' ) ein, dann erhält man einen Zusammenhang zwischen der Gegenstandweite s1 am Eingang des Linsensystems und der Bildweite s2' am Ausgang. Die Angelegenheit ist etwas unübersichtlich, aber wir müssen es einmal hinschreiben: |
||||||||||||||||||||
| So, das ist jetzt der oben angekündigte Zusammenhang zwischen der Bildweite s2' am Ausgang des Linsensystems und der Gegenstandsweite s1 am Eingang. Etwas unübersichtlich, aber das werden wir gleich vereinfachen |
1/s2' = 1/f2 - (1-f1/s1) / (d - f1 - d.f1/s1)
Brauchen Sie nicht nachzurechnen - können Sie mir glauben ! |
||||||||||||||||||||
| s1 gegen Unendlich heisst - in dem obigen Ausdruck gehen "f1/s1" und "d.f1/s1" gegen Null. | Wenn wir nun die Gegenstandsweite s1 gegen Unendlich gehen lassen, - was nichts anderes bedeutet, als das wir das einfallende Licht parallel machen -, dann ist die Bildweite s2' am Ausgang des Linsensystems identisch mit der bildseitigen Brennpunktabstand fsys'.
1/fsys' = (d - f1 - f2) / (d - f1) . f2 |
||||||||||||||||||||
| Ganz analog lässt sich ein Ausdruck für die gegenstandsseitige Brfennpunktabstand fsys bestimmen:
1/fsys = (d - f1 - f2) / (d-f2) . f1 |
|||||||||||||||||||||
| Zum Abschluss unserer Überlegungen lassen wir nun noch den Abstand d zwischen den Linsen verschwinden ( d = 0 !) - d.h. die Linsen rutschen ganz dicht zusammen - und wir erhalten sowohl für den gegenstandsseitigen Brennpunktabstand fsys als auch für den bildseitigen Brennpunktabstand fsys' des Linsensystems den Ausdruck:
1/fsys = 1/ fsys' = (f1+f2) / f1 . f2 |
|||||||||||||||||||||
| Jetzt wird endlich der tiefere Sinn deutlich, der hinter der Definition der Dioptrie steckt. Da die Dioptrie - d.h. die Brechkraft - als Kehrwert der Brennweite definiert ist, kann man die Brechkraft eines Systems, das aus mehreren Linsen besteht, einfach durch Addition der Dioptriewerte der Einzellinsen erhalten, und muß nicht erst umständlich den Kehrwert berechnen. (Voraussetzung ist selbstverständlich, daß es sich um 'dünne' Linsen handelt !) | ... und jetzt wird auch deutlich, warum wir uns bei den letzten drei Gleichungen immer mit den Reziprokwerten herumgequält haben, die letzte Beziehung lässt sich nämlich noch etwas schöner schreiben:
1/fsys = 1/f1 + 1/f2 oder für mehrere dünne Linsen: 1/fsys = 1/f1 + 1/f2 + 1/f3 + ..... |
||||||||||||||||||||
| D.h., man kann mehrere dünne Linsen 'hintereinanderschalten' und dann aus der Summe der Kehrwerte für die Einzelbrennweiten die Gesamtbrennpunktabstand bestimmen. | |||||||||||||||||||||
| Beispiel: | Nehmen wir 'mal an, Sie packen zwei dünne Linsen mit gleicher Brennweite f möglichst dicht zusammen. Wie groß ist der Brennpunktabstand fsys von beiden zusammen ? Na, ganz einfach :
1/fsys = 1/f + 1/f = 2/f, oder: fsys = f/2 Sie haben es sicher bereits geahnt, und das obige Interaktive Bildschirm-Experiment "Abbildung durch zwei dünne Linsen" hat es ja auch bereits deutlich gemacht, - der Brennpunktabstand hat sich halbiert. |
||||||||||||||||||||
| In den folgenden Interaktiven Bildschirm-Experimenten wollen wir die Sache mit dem Brennpunktabstand eines Systems von zwei Linsen noch etwas vertiefen. Zu diesem Zweck habe ich dafür gesorgt, dass von der linken Seite ein paralleles LIchtstrahlenbündel auf die Linsen trifft. Durch Verschieben der Linsen und durch Veränderung der Brennweiten kann die Lage des Brennpunktes auf der rechten Seite des Linsensystems verändert werden | |||||||||||||||||||||
| Sie können sowohl die Position der beiden Linsen, als auch deren Brennweite verändert. Klicken Sie dazu bitte mit der linken Maustaste auf einen der farblich hervorgehobenen Punkte, halten Sie die Maustaste gedrückt und bewegen Sie die Maus. | |||||||||||||||||||||
| Brennpunkt eines Zwei-Linsen-Systems.
Bitte beachten Sie folgenden Sonderfall: Wenn Sie den Abstand der Linsen so wählen, dass er genau der Summe der Einzelbrennweiten entspricht, dann existiert kein Systembrennpunkt, d.h. das Strahlenbündel tritt parallel ein und wieder parallel aus. Es handelt sich um einen sog. teleskopischen Strahlengang. Neben der Verwendung als Fernrohr - wir kommen noch darauf zurück - dient eine solche Linsenanordnung zur Erhöhung bzw.Verringerung der Leuchtdichte des austretenden Parallelstrahls. Durch Einstellung eines geeigneten Brennweitenverhältnisses, kann das Verhältnis der beiden Strahldurchmesser, und damit die Leuchtdichte des austretenden Strahls beeinflusst werden. Dieses Prinzip wird z.B. verwendet, um ein paralleles LIchtbündel mit grossem Durchmesser möglichst ohne Verluste in einen (sehr dünnen !) Lichtleiter einzukoppeln. |
|||||||||||||||||||||
| Die geometrische Optik lebt von Vereinfachungen. Ich habe das bereits im Kapitel 1 angesprochen - diesen auf eine Linie zusammengezogenen "Lichtstrahl" den wir hier immer verwenden gibt es eigentlich gar nicht. (Viel eher ein Wellenfeld mit einer stark ausgeprägten Richtcharakteristik.) - Aber das stört uns "Optiker" nicht weiter ! Oder ? | |||||||||||||||||||||
| "Dicke" Linsen sind, - wie der Name schon sagt - , das Gegenteil von "dünnen" Linsen. "Dicke" Linsen lassen sich nicht einfach durch eine Mittelebene ersetzten, weil der Linsenkörper zwischen Vorder- und Rückseite so dick ist, dass dies für die Bestimmung des Strahlverlaufes berücksichtigt werden muss. | Eine weitere Vereinfachung im Umgang mit "dicken Linsen" und komplexen Linsensystemen soll jetzt angesprochen werden. Wir haben bei "dünnen" LInsen den eigentlichen Linsenkörper vernachlässigt und die Ablenkung des Lichtstrahls immer an einer (fiktiven ?) Mittelebene beginnen lassen. (Schauen Sie sich den Strahlverlauf durch eine "dünne" Linse darauf noch 'mal an.)
Die folgende Skizze zeigt das Prinzip:
|
||||||||||||||||||||
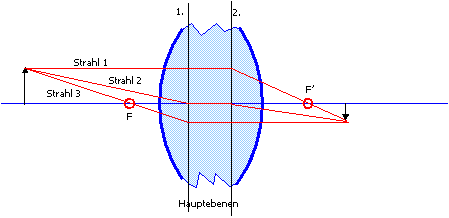
| Hauptbenen bei einer dicken Linse:
Zur Konstruktion des Abbildungsstrahlengangs verfährt man , wenn Hauptbenen vorhanden sind, auf folgende Weise: Der parallel zur optischen Achse einfallende Strahl 1 auf der linken Seite wird bis zu 2. Hauptbene verlängert und dort zum Brennpunkt F' hin gebrochen. Der sog. Mittelpunktstrahl (Strahl 2) wird bis zum Fußpunkt der Hauptebene 1 gezogen, parallel zur optischen Achse weitergeführt und an Hauptebene 2 parallel zum einfallenden Strahl 2 weitgegeführt. Der Strahl 3 durch den linken Brennpunkt wird bis zur Hauptebene1 gezogen und von dort parallel zur optischen Achse weitergeführt. |
|||||||||||||||||||||
| Die genaue Berechnung an welcher Stelle im Glaskörper der "dicken" Linse die Hauptebenen zu suchen sind wollen wir uns an dieser Stelle ersparen. ( Für den Spezialfall einer symmtrischen Bikonvexlinse hat jede Hauptebene vom nächst gelegenen Scheitel der Linse - in etwa - den Abstand
d / 2n Dabei ist 'd' die Dicke der Linse in der Mitte und 'n' der Brechungsindex.) |
|||||||||||||||||||||
|
Das Konzept der Hauptebene lässt sich auch auf ein System von dünnen Linsen anwenden. Das folgende interaktive Bildschirmexperiment soll das verdeutlichen: |
|||||||||||||||||||||
| Sie können sowohl die Position der beiden Linsen, als auch deren Brennweite verändert. Klicken Sie dazu bitte mit der linken Maustaste auf einen der farblich hervorgehobenen Punkte, halten Sie die Maustaste gedrückt und bewegen Sie die Maus. |
|
||||||||||||||||||||
| Ich muß mich an dieser Stelle bei einem aufmerksamen Leser dieser Seiten bedanken:
Die hier definierte Systembrennweite ist nicht identisch mit dem oben beschriebenen Brennpunktabstand von der bildseitigen Linse ! In einer früheren Version dieses Textes hatte ich die beiden Begriffe nicht auseinander gehalten und damit wohl etwas Verwirrung gestiftet - tut mir leid ! |
Hauptebene eines Systems aus zwei 'dünnen' Bikonvexlinsen : Zur Bestimmung der bildseitigen Hauptebene wird der ( von der linken Seite) parallel zur optischen Achse einfallende LIchtstrahl bis zum Ausgang des Linsensystems (auf der rechten Seite) verlängert. Der Schnittpunkt mit dem aus dem Linsensystem austretenden Strahl definiert dann die Position der Hauptebene. (Für die gegenstandsseitige Hauptebene müsste der Strahlverlauf umgekehrt werden.) Der Schnittpunkt des aus dem Linsensystem austretenden Strahls mit der optischen Achse ergibt den Brennpunkt des Linsensystems (Systembrennpunkt) Die Systembrennweite ist definiert als der Abstand des Systembrennpunktes von der zugehgörigen Hauptebene. Wenn Sie im oben gezeigten Linsensystem 'mal etwas herumspielen, also den Abstand und die Brennweiten der Linsen verändern, dann werden Sie feststellen, dass Sie nicht nur die Lage des Systembrennpunktes, sondern auch die der Hauptebene und damit die Systembrennweite sehr weitgehend verändern können. Versuchen Sie 'mal Folgendes: schieben Sie mit der Maus den Brennpunkt F1' von Linse 1 so dicht wie möglich an den Brennpunkt F2 von Linse 2 heran. Sie können dabei beobachten wie sich die (bildseitige) Hauptebene immer weiter nach links verschiebt bis sie schliesslich sogar auf der anderen Seite - der Gegenstandsseite - des Linsensystems ankommt und schliesslich im Nirwana verschwindet. |
||||||||||||||||||||
|
Wir kommen damit zu einem erstaunlichen Ergebnis. |
|||||||||||||||||||||
|
zurück zum Inhaltsverzeichnis |
|||||||||||||||||||||